Задания для школьной олимпиады по математике, 6 — 10 классы

Школьная олимпиада

7 класс

1. Среди семи внешне одинаковых монет есть одна фальшивая – более лёгкая по весу. Как при помощи всего двух взвешиваний на чашечных весах (без гирь) определить фальшивую монету?

2. Пассажир проезжая в трамвае, заметил знакомого, который шёл вдоль линии трамвая в противоположную сторону. Через 10 секунд пассажир вышел из трамвая и пошёл догонять своего знакомого. Через сколько секунд он догонит знакомого, если он идёт в два раза быстрее знакомого и в 5 раз медленнее трамвая?

3. р, р + 10, р + 14 – простые числа. Найдите р.

4. Разделите участок земли, имеющий форму квадрата, на 4 равные части одинаковой формы и размера так, чтобы в каждую часть попало ровно по одному из 4 растущих на участке деревьев.

5. 12 моих одноклассников любят читать детективы, 18 – фантастику, 3 – с удовольствием читают и то, и другое, а 1 вообще ничего не читает. Сколько учеников в нашем классе?

6. РЕШИ + ЕСЛИ = СИЛЁН

Восстановите запись, если разным буквам соответствуют разные цифры, одинаковым – одинаковые, при условии, что наибольшая цифра в записи числа «СИЛЁН» равна 5.

Школьная олимпиада

6 класс

1. Разность двух чисел на 17 меньше уменьшаемого и на 9 больше вычитаемого. Найдите уменьшаемое и вычитаемое. 

2. Нужно разместить 17 кроликов так, чтобы в каждой клетке было разное количество кроликов. Какое наибольшее число клеток понадобится? 

3. В один сосуд входит 3л, а в другой 5л. Как с помощью этих сосудов налить в кувшин 4л воды из водопроводного крана?

4. На плакате разными способами написаны четыре числа.(2б.)

77556644

99778866

23339977

55447722

Известно, что:

• число, написанное фломастером, расположено выше числа, написанного пером;

• написанное карандашом – левее написанного углем;

• написанное углем – ниже написанного пером;

• написанное углем – выше написанного карандашом.

5. Будет ли сумма чисел 1 + 2 + 3 + ……+ 2005 + 2006 + 2007 делиться на 2007?
   Ответ обоснуйте. 

6. Все треугольники, изображенные на рисунке, имеют равные стороны.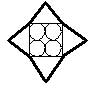
    Радиус каждой из окружностей равен 2 см.
   Окружности касаются друг друга и сторон квадрата.
   Чему равен периметр звездочки, нарисованной жирной линией?

Школьная олимпиада

8 класс

1. Когда Винни-Пух пришел в гости к Кролику, он съел 3 тарелки меда, 4 тарелки сгущенки и 2 тарелки варенья, а после этого не смог выйти наружу из-за того, что сильно растолстел от такой еды. Но известно, что если бы он съел 2 тарелки меда, 3 тарелки сгущенки и 4 тарелки варенья или 4 тарелки меда, 2 тарелки сгущенки и 3 тарелки варенья, то спокойно смог бы покинуть нору гостеприимного Кролика. От чего больше толстеют: от варенья или от сгущенки?

2.  В трех кучках лежат соответственно 12, 24 и 19 спичек. За ход можно переложить спичку из одной кучки в другую. За какое наименьшее число ходов можно получить три кучки с 8, 21 и 26 спичками?

3. Нарисуйте на плоскости пять различных прямых так, чтобы они пересекались ровно в семи различных точках.

4. Мальчик пошел с отцом в тир. Отец купил ему 10 пулек. В дальнейшем отец за каждый промах отбирал у сына одну пульку, а за каждое попадание давал одну дополнительную пульку. Сын выстрелил 55 раз, после чего пульки у него кончились. Сколько раз он попал?

5. Что больше: ?

6. Разложите на множители выражение: .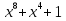

Школьная олимпиада

9 класс

1. Петя купил общую тетрадь объёмом 96 листов и пронумеровал все страницы от 1 до 192. Его младший брат вырвал из тетради все листы и разбросал по комнате. Петя подобрал наугад с пола 25 листов и сложил все 50 чисел, которые на них написаны. Могло ли у него получится 2006?

2. В некоторой трапеции длина одной из диагоналей равна сумме длин оснований трапеции, а угол между диагоналями равен 60°. Доказать, что трапеция равнобокая.

3. Доказать, что уравнение

(х – а) (х – b) + (x – b)  (x – c) + (x – c)  (x – a) =0

имеет действительные корни при любых действительных числах a, b, c.

4. На дискотеке было 20 танцующих. Мария танцевала с семью танцорами, Ольга – с восемью, Вера – с девятью и т.д. до Нины, которая танцевала со всеми танцорами. Сколько танцоров (парней) было на дискотеке?

5. Клетки квадрата 15  15 раскрашены в красный, синий и зелёный цвета. Докажите, что найдутся по крайней мере две строки, в которых клеток хотя бы одного цвета будет поровну.

6. Постройте график функции .

Школьная олимпиада

10 класс

1. . Постройте эскиз графика функции: .
   
   
   

2. Периметр треугольника равен 24см. Можно ли около этого треугольника описать окружность радиусом 5см?

3. В каком году ХХ века родился человек, если в 1997 году произведение цифр лет, прожитых им, уменьшенное в 4 раза, на 3 меньше суммы цифр года его рождения?

4. Найдите площадь фигуры, заданной неравенством:

|х — 5| + |у + 9|

5. Решите систему уравнений

6. Упростите выражение , где 0° < α < 90°, считая, что корень означает арифметическое значение квадратного корня.