Хостинг документов » 8 класс » Внеклассное мероприятие «Великая загадка природы» 8 класс

Внеклассное мероприятие «Великая загадка природы» 8 класс

Внеклассный час- ток-шоу по биологии для 8 класса

Пусть говорят

Тема: Великая загадка природы.

Работу выполнила

учитель биологии и химии

МОУ ООШ №12 г. Бугульмы, РТ

Балаболина Екатерина Анатольевна

20011- 20012 уч. Год

Эту тему я решила разработать после того, как прочла книгу Дэна Брауна «Код да Винчи» Эта книга стала бестселлером 21-го века.

В одной из глав герой книги профессор Лэнгдон вспоминает о своих лекциях по Золотому Сечению для студентов Гарвардского университета. Лэнгдон учит студентов:

«Несмотря на почти мистическое происхождение, число PHI сыграло по-своему уникальную роль. Роль кирпичика в фундаменте построения всего живого на земле. Все растения, животные и даже человеческие существа наделены физическими пропорциями, приблизительно равными корню от соотношения числа PHI к 1. Эта вездесущность PHI в природе … указывает на связь всех живых существ. Раньше считали, что число PHI было предопределено Творцом вселенной. Ученые древности называли одну целую шестьсот восемнадцать тысячных «божественной пропорцией».

Наверняка всем нам не раз приходилось задумываться о том, почему Природа способна создавать такие удивительные гармоничные структуры, которые восхищают и радуют глаз. Почему художники, поэты, композиторы, архитекторы создают восхитительные произведения искусства из столетия в столетие. В чем же секрет и какие законы лежат в основе этих гармоничных созданий? В течение тысячелетий многие мыслители искали ответ на этот вопрос. И большинство из них пришло к заключению, что в мире царит Всеобщая Гармония, основанная на Золотом Сечении.

Не одно столетие ученые применяют уникальные математические свойства числа PHI и эти исследования продолжаются и в наши дни. Это число нашло широкое применение во всех областях современной науки, включая физику, астрономию, кристаллографию, ботанику, биологию, медицину, психологию, геологию, экономику и все виды искусств.

Но о Золотом Сечении мало кто знает. С этой информацией не знакомят в школе.

Возможно, дело в традиции. Традиционно классическая наука, а следовательно, и классическая педагогика, относилась к «Золотому Сечению» с некоторым предубеждением. Все дело в широком использовании Золотого Сечения в астрологии и так называемых «эзотерических науках». И «материалистическое образование» выбросило Золотое Сечение вместе с астрологией на свалку сомнительных научных концепций. Результат налицо: большинство так называемых «образованных» людей хорошо знают теорему Пифагора, но имеет весьма смутное представление о Золотом Сечении. А ведь Золотое Сечение вместе с теоремой Пифагора принадлежат к двум главным «сокровищам геометрии»! А это означает, что изучению уникальных свойств и применений Золотого Сечения в окружающем нас мире надо уделять в образовании не меньшее внимание, чем теореме Пифагора.

Подготовка к мероприятию:

Для проведения мероприятия нужна подготовка. Необходимо выбрать учащихся, которые будут участниками шоу. Остальные дети класса будут выступать в роли зрителей. Участникам нужно дать задания найти информацию по данной теме из различных источников. Это могут быть книги по математике, искусству, биологии, истории а так же ресурсы интернета. К этой работе можно подключить так же и учащихся, выступающих в роли зрителей. Учителя- предметники тоже могут помочь в сборе информации. Весь собранный материал затем нужно будет систематизировать и распределить по ролям.

Свое внеклассное мероприятие я решила провести в виде ток-шоу «Пусть говорят». Оформление зала, где проходит ток-шоу: в центре класса- место для героя программы. Так же предусмотрены места для гостей программы и зрителей. На стенах- высказывания выдающихся людей на тему Золотого Сечения, так же необходим компьютер и проектор для показа презентации.

В ход мероприятия можно включать музыкальные паузы. Музыкальные номера исполняют дети из других (возможно, более младших) классов. Помимо музыкальных заставок можно использовать другие номера художественной самодеятельности для того, что бы игра стала более зрелищной.

В конце мероприятия проводится викторина для зрителей, состоящая из 7 вопросов по теме золотого сечения.

Цель: Стимулировать учащихся к получению новых знаний; расширять кругозор, повышать интерес к предмету; развивать логическое мышление, умение устанавливать причинно-следственные связи, умения рассуждать и делать выводы, показать связь биологии с другими естественными науками. формирование у обучающихся понимания единства человека и природы.

Оформление: Выставка фотографий с изображениями различных растений, животных; рисунок Леонардо Да Винчи «Виртувианский человек», Картина И. И. Шишкина «Сосновая роща»; Высказывания выдающихся людей:

Геометрия владеет двумя сокровищами: одно из них — это терема Пифагора, а другое — деление отрезка в среднем и крайнем отношении…Первое можно сравнить с мерой золота, второе же больше напоминает драгоценный камень.

И. Кеплер

Природа ничего не делает напрасно и не достигает с помощью многого того, что можно было достигнуть с помощью немногого.

И.Ньютон

Ход мероприятия

Ведущий: Здравствуйте! Сегодня у нас программа «Пусть говорят», и с вами я-…

Недавно на экраны всего мира вышел одноименный фильм по мотивам произведения английского писателя Дэна Брауна «Код да Винчи». Эта книга стала бестселлером 21-го века. В одной из глав герой книги профессор Лэнгдон вспоминает о своих лекциях по Золотому Сечению для студентов Гарвардского университета. Лэнгдон учит студентов:

Итак, тема нашей сегодняшней встречи: «Великая загадка природы»

Наверняка все нам не раз приходилось задумываться о том, почему Природа способна создавать такие удивительные гармоничные структуры, которые восхищают и радуют глаз. Почему художники, поэты, композиторы, архитекторы создают восхитительные произведения искусства из столетия в столетие. В чем же секрет и какие законы лежат в основе этих гармоничных созданий?

Для того что бы разобраться в этих вопросах мы пригласили в студию гостей:

-Математик

-Ботаник

-Зоолог

-Анатом

-Креационист

— Исскуствовед

— Историк

— Физик.

В кресле главного героя Фома Неверующий: человек, который не верит ни чему и ни кому. И, конечно же, не верит он и в существование Золотой пропорции.

И первый мой вопрос к историку: скажите, давно ли известно о существовании золотого сечения?

Историк: В течение тысячелетий многие мыслители, начиная с Пифагора и Платона и заканчивая Лосевым и Флоренским, искали ответ на этот вопрос. И большинство из них пришло к заключению, что в мире царит Всеобщая Гармония, основанная на Золотом Сечении.

Золотое Сечение, называемое также числом PHI или Ф в честь великого древнегреческого скульптора Фидия (Phidius), который использовал это число в своих скульптурах, пронизывает всю историю искусства.

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Kвадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида.

В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре. Леонардо да Винчи, художник и ученый, также много внимания уделял изучению золотого деления. Он видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Kнига была восторженным гимном золотой пропорции. Cреди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» Леонардо да Винчи ввел название золотое сечение. Так оно и держится до сих пор как самое популярное.

Над теми же проблемами трудились и другие выдающиеся ученые: немец Альбрехт Дюрер, Великий астроном XVI в. Иоган Кеплернемецкий, исследователь золотого сечения профессор Цейзинг.

В конце XIX – начале XX вв. появилось немало чисто формалистических теории о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели и т.д.

Не одно столетие ученые применяют уникальные математические свойства числа PHI и эти исследования продолжаются и в наши дни. Это число нашло широкое применеие во всех областях современной науки, включая физику, астрономию, кристаллографию, ботанику, биологию, медицину, психологию, геологию, экономику и все виды искусств.

Свежие документы: Образ «маленького человека» в повести Н.В. Гоголя «Шинель» 8 класс

Ведущий: Спасибо.

Фома Неверующий: Невероятно! Но почему же я об этом не знал раньше? Почему же с такой интересной информацией меня не ознакомили в средней школе? Может, это все выдумки?

Ведущий: Действительно. Ведь знания о Золотом Сечении и о его многочисленных приложениях в Природе, Науке и Искусстве, несомненно, обогатили бы каждого из нас.

Историк: Вряд ли кто-либо из признанных ученых в области педагогики сможет дать вразумительный ответ на этот вопрос. Возможно, дело в традиции. Традиционно классическая наука, а следовательно, и классическая педагогика, относилась к «Золотому Сечению» с некоторым предубеждением. Все дело в широком использовании Золотого Сечения в астрологии и так называемых «эзотерических науках». И «материалистическое образование» выбросило Золотое Сечение вместе с астрологией на свалку сомнительных научных концепций. Результат налицо: большинство так называемых «образованных» людей хорошо знают теорему Пифагора, но имеет весьма смутное представление о Золотом Сечении.

Математик: Золотое Сечение вместе с теоремой Пифагора принадлежат к двум главным «сокровищам геометрии»! А это означает, что изучению уникальных свойств и применений Золотого Сечения в окружающем нас мире надо уделять в образовании не меньшее внимание, чем теореме Пифагора. И тогда вполне возможно, что изучение математики, которую в своем большинстве ученики рассматривают как сухую и неинтересную дисциплину, неожиданно могло бы превратиться в увлекательный поиск математических закономерностей окружающего нас мира. То есть введение Золотого Сечения в математическое образование поднимает интерес учащихся к изучению математики!

Ведущий: Тогда еще один вопрос к вам: а что такое это золотое сечение? Думаю, вы лучше всех сможете объяснить.

Математик: Золото́е сече́ние (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление, φ) — деление отрезка на части в таком соотношении, при котором меньшая часть относится к большей, как большая ко всему в целом. Например, деление отрезка АС на две части таким образом, что большая его часть АВ относится к меньшей ВС так, как весь отрезок АС относится к АВ (т. е. |АВ| / |ВС| = |АС| / |АВ|).

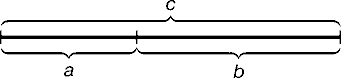
Эту пропорцию принято обозначать греческой буквой φ и она равна:

Отрезки золотой пропорции выражаются бесконечной иррациональной дробью 0,618…, если c принять за единицу, a = 0,382. Числа 0.618 и 0.382 являются коэффициентами последовательности Фибоначчи. На этой пропорции базируются основные геометрические фигуры.

Ведущий: А что такое последовательность Фибоначчи?

Фома Неверующий: Это полная ерунда, выдуманная неизвестно зачем…

Математик: Нет, не ерунда. И проверить это просто.

Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих.

Ведущий: Давайте попросим нашего героя самого сделать все расчеты. Может, тогда он изменит свою позицию?

Фома: Запросто: 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д.,

Математик: В числах Фибоначчи существует одна очень интересная особенность. При делении любого числа из последовательности на число, стоящее перед ним в ряду, результатом всегда будет величина, колеблющаяся около иррационального значения 1.61803398875… и через раз то пpевосходящая, то не достигающая его.

Фома: 21 : 34 = 0,617, а 34 : 55 = 0,618. Действительно так…

Математик: Это отношение обозначается символом Ф. Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.

Б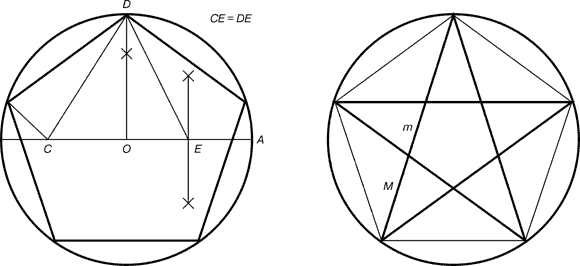олее того, после 13-ого числа в последовательности этот результат деления становится постоянным до бесконечности ряда… Именно это постоянное число деления в средние века было названо Божественной пропорцией, а ныне в наши дни именуется как золотое сечение, золотое сpеднее или золотая пропорция.

Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой.

Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.

В геометрии прямоугольник с таким отношением сторон стали называть золотым прямоугольником. Его длинные стороны соотносятся с короткими сторонами в соотношении 1,168 : 1.

Фома: Ну хорошо, убедили. Но только в том, что Золотое сечение существует. Но какое оно имеет отношение к природе?

Ведущий: А вот об этом мы спросим у наших гостей: ботаника и зоолога.

Зоолог: Членение «по Фибоначчи» весьма распространено среди различных типов животных, включая членистоногих, насекомых, черепах и высших животных. В процессе эволюции тело членистоногих разделилось на три отдела: головной, грудной и брюшной. Для всего животного мира характерны симметрия форм и наличие парных органов, членение на три части тела (голова, грудь, брюшко), членение конечностей на 3 и 5 частей, а брюшка — на 3. Это является характерной чертой морфологии насекомых.

Строение форм представителей более высокого уровня животного мира также подчиняется закону чисел Фибоначчи. Так у черепахи в панцире имеется 13 сросшихся роговых пластин, из них 5 пластин в центре, а 8 по краям, на лапках 5 пальцев, а позвоночник содержит 34 позвонка. У гавиалового крокодила Малайского архипелага вдоль туловища расположены 55 роговых пластин. На теле кавказской носатой гадюки также 55 темных пятен, а в скелете габонской гадюки насчитали 144 позвонка. У высших типов животных на нашей планете — млекопитающих — имеются аналогичные закономерности членения тела. Число костей скелета в различных частях тела у самых разнообразных животных близко к 13 (кит, верблюд, олень, тур и т.д.), число позвонков близко к 34 и 55. Так, у гигантского оленя 34 позвонка, у кита — 55. В процессе эволюции происходило усложнение организмов, что вызывало увеличение количества частей тела и костей в скелете. Этот процесс осуществлялся не только непрерывно, но и дискретно, следуя некоторому «плану эволюции по Фибоначчи». У некоторых моллюсков количество частей, формирующих конические раковины, отвечает числам Фибоначчи.

Раковины фораминифер имеют 13 частей, раковины шпорцевой улитки — 8, количество камер раковины наутилуса — 34, тело наутилоидей делится на 13 частей, раковина гигантской тридакны собрана в 5 складок. Число ребер ископаемой раковины брахиопод равно 34. Такое же количество ребер имеют крохотные раковины тектакулитов. По краям пятнистой раковины ципреи из Индийского океана расположены мелкие зубцы, количество которых равно 21. Из приведенных примеров видно, что конструкции раковин многих ископаемых и современных моллюсков предпочитают числа 5, 8, 13, 21, 34.

Таким образом, золотое сечение, числа Фибоначчи и пентагональная симметрия являются бесспорным элементом роста живых существ.

Ботаник: Но еще более убедительной демонстрацией проявления золотого сечения в мире растений является явление «филлотаксиса»

Спирали широко проявляют себя в живой природе. Спирально закручиваются усики растений, по спирали происходит рост тканей в стволах деревьев, по спирали расположены семечки в подсолнечнике, спиральные движения (нутации) наблюдаются при росте корней и побегов. Очевидно, в этом проявляется наследственность организации растений, а ее корни следует искать на клеточном и молекулярном уровне.

Пяти-лепестковыми являются цветы кувшинки, шиповника, боярышника, гвоздики, груши, черемухи, яблони, земляники и многих других. Оказывается, что расположение листьев на стеблях также носит строгий математический характер и это явление называется в ботанике «филлотаксисом». Суть филлотаксиса состоит в винтовом расположении листьев на стебле растений (ветвей на деревьях, лепестков в соцветьях и т.д.). Рассмотрим, например, расположение листьев на стебле растения. Мы видим, что листья находятся на различных высотах стебля вдоль винтовой линии, обвивающейся вокруг его поверхности. Для того чтобы перейти от нижележащего листа к следующему, приходится мысленно повернуть лист на некоторый угол вокруг вертикальной оси стебля, а затем поднять его на определенный отрезок вверх. В этом и состоит суть «винтовой симметрии».

Фома: Я понял. Получается, это действительно правда. И золотое сечение не выдумка автора «Кода да Винчи»… Но человек ведь тоже часть живой природы. Неужели и в его строении есть такие же закономерности?

Ведущий: Думаю, что ученый-анатом подтвердит это?

Анатом: Многие пропорции человеческого тела можно выразить отношением небольших целых чисел, если пренебречь некоторой погрешностью. Для этого можно воспользоваться средними статистическими (антропометрическими) данными населения нашей страны. Эти данные для мужчин и женщин существенно различаются и приводятся раздельно. Вот некоторые из них (для мужчин и женщин): рост 1680 и 1567, длина руки — 723 и 661, длина ноги — 900 и 835, высота линии талии — 1035 и 976, высота колена — 506 и 467, ширина плеч — 380 и 349, рост сидя — 1310 и 1211, длина бедра — 590 и 568 мм. Используя эти статистические данные, можно рассчитать пропорции различных частей тела, например, по отношению к росту человека. Полученные таким образом пропорции оказались очень близкими к целочисленным отношениям. Среднее отклонение целочисленных отношений от действительных составляет всего 0,6%. Похоже, что и здесь «правят» целые числа.
Характерно, что размеры частей тела мужчин и женщин существенно различаются, но отношения этих частей отвечают в большинстве случаев отношениям тех же целых чисел. Характерно также, что усредненные величины рассчитанных характеристик отдельно для мужчин и женщин оказываются более близки к целочисленным отношениям. Создается впечатление, что пропорции мужских и женских тел как бы отклоняются в разные стороны от пропорций некоторого «идеального» бесполого человеческого тела. Соотношение среднего роста мужчин и женщин составляет 1,072, что очень близко 15/14. Такое же в среднем отношение всех остальных частей мужского и женского тел. Довольно точно отвечает рисункам мужских фигур Леонардо да Винчи и Микеланджело. Однако на других фигурах она не оправдывается. Да и неудивительно, ведь конституция тел очень различна, даже гармонично развитые тела могут быть узкоплечими и широкоплечими. Давно уже существует мнение, что пятилучевая симметрия, столь характерная для мира растений и животных, проявляется и в строении человеческих тел. И человеческое тело можно рассматривать как пятилучевое, где лучами служат голова, две руки и две ноги. В связи с этим многие исследователи математических закономерностей тела человека вписывали его в пентаграмму. Так назвали позу человека с раздвинутыми на 180° руками и разведенными на 90° ногами. Такая модель нашла отражение и в построениях Леонардо да Винчи и Дюрера.

Свежие документы: Конспект урока на тему: «Генетика человека»

Займемся «инвентаризацией» частей человеческого тела. У него одно туловище, одна голова, одно сердце и т. д.; многие части тела и органы парные, например, руки, ноги, глаза, почки. Из трех частей состоят ноги, руки, пальцы рук. На руках и ногах по пять пальцев, а рука вместе с пальцами состоит из восьми частей. У человека 12 пар ребер (одна пара атрофирована и присутствует в виде рудимента). Очевидно, в прошлом у человека было 13 пар ребер, но в процессе эволюции, при переходе к прямостоячему положению количество ребер уменьшилось. Характерно, что у млекопитающих (коровы, овцы, собаки, кошки и др.) по 13 пар ребер. Число молочных зубов у ребенка равно 20, а у взрослого достигает 32, причем последняя пара («зубы мудрости») появляется позже других и не у всех людей.
И вот что интересно: общее число костей скелета человека близко к 233, то есть отвечает еще одному числу Фибоначчи.
Трудно предположить, что все это лишь случайное совпадение. Более очевидно наличие определенной закономерности развития организма, закономерного итога его эволюции от простейших по строению далеких предков до «вершины эволюции» — человека.

Но фибоначчиева закономерность характерна не только для костей. Например, в строении головного мозга различают семь частей. В основании головного мозга выделяют 8 частей, выполняющих разные функции. В теле человека насчитывается 8 различных желез внутренней секреции. Кишечник и соседние с ним органы (желудок, печень, желчный пузырь и т.д.) составляют в сумме 13 органов. Дыхательные органы человека состоят из 8 частей. Печень также состоит из 8 частей; почки состоят из 5 частей, а сердце из 13.

Случайно ли это? Скорее всего — нет. Человек, как и другие творения природы, подчиняется всеобщим законам развития. Корни этих законов нужно искать глубже — строении клеток, хромосом и генов, а далее — в возникновении самой жизни на Земле.

В теле человека насчитывают около 630 мышц, составляющих около 0,4 массы тела человека. Как тут не вспомнить, что 610 является числом Фибоначчи, а 0,38 отвечает золотой пропорции в делении целого на части. Делая первый шаг, человек приводит в движение около 300 мышц, в том числе 144 на позвоночном столбе (144 — число Фибоначчи), 20 — удерживающих в равновесии голову. От головного мозга человека отходит 12 пар нервов, а от спинного — 31 пара.

Этот список частей тела человека можно продолжить. Нетрудно видеть, что в их перечне очень часто встречаются числа Фибоначчи или близкие к ним величины. Ими буквально «нашпиговано» тело человека. Но ведь ряд этих чисел не только отражает дискретный характер роста и членения целого на части, но и отвечает золотой пропорции. Отношение рядом стоящих чисел Фибоначчи приближается к золотой пропорции, значит, и соотношения чисел различных органов часто отвечает золотой пропорции. Золотая пропорция как невидимый, но строгий дирижер, взмахами волшебной палочки эволюции отсчитывает числа органов человека и числа частей в этих органах.

Ведущий: Ну, Фома Неверующий, Убедили вас ответы наших гостей?

Фома: Почти. Все сказанное звучит достаточно убедительно. Но мне хотелось бы самому убедиться в том что это правда.

Ведущий: Тогда, может быть, дать вам линейку и вы замерите всех присутствующих в зале?

Анатом: В строении черт лица человека также есть множество примеров, приближающихся по значению к формуле золотого сечения. Однако не бросайтесь тотчас же за линейкой, чтобы обмерять лица всех людей. Потому что точные соответствия золотому сечению, по мнению ученых и людей искусства, художников и скульпторов, существуют только у людей с совершенной красотой. Собственно точное наличие золотой пропорции в лице человека и есть идеал красоты для человеческого взора.

К примеру, если мы суммируем ширину двух передних верхних зубов и разделим эту сумму на высоту зубов, то, получив при этом число золотого сечения, можно утверждать, что строение этих зубов идеально.

На человеческом лице существуют и иные воплощения правила золотого сечения. Приведем несколько таких соотношений:
Высота лица / ширина лица,
Центральная точка соединения губ до основания носа / длина носа.
Высота лица / расстояние от кончика подбородка до центральной точки соединения губ
Ширина рта / ширина носа,
Ширина носа / расстояние между ноздрями,
Расстояние между зрачками / расстояние между бровями.

Фома: Ну дома-то я обязательно проверю это на всех своих родственниках.

Ведущий: Есть ли в строении тела человека еще примеры Золотого сечения?

Анатом: Конечно! Достаточно лишь приблизить сейчас вашу ладонь к себе и внимательно посмотреть на указательный палец, и вы сразу же найдете в нем формулу золотого сечения. Каждый палец нашей руки состоит из трех фаланг.

Сумма двух первых фаланг пальца в соотношении со всей длиной пальца и дает число золотого сечения (за исключением большого пальца).

Кроме того, соотношение между средним пальцем и мизинцем также равно числу золотого сечения.

У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, то есть всего 10, но за исключением двух двухфаланговых больших пальцев только 8 пальцев создано по принципу золотого сечения. Тогда как все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи.

Ведущий: В нашей студии сегодня присутствует и искусствовед. Вам тоже есть чем поделиться с нами?

Искусствовед: Да. Представьте себе, что Пирамида Хеопса, самая известная из Египетских пирамид, знаменитый греческий храм Парфенон, большинство греческих скульптурных памятников, непревзойденная «Джоконда» Леонардо да Винчи, картины Рафаэля, Шишкина и современного русского художника Константина Васильева, этюды Шопена, музыка Бетховена, Чайковского и Бэллы Барток, «Модулор» Корбюзье, стихи Пушкина и Шота Руставли — вот далеко не полный перечень выдающихся произведений искусства, наполненных чудесной гармонией, основанной на Золотом Сечении. Общепринято мнение, что золотая пропорция является не только мерилом гармонии в природе и в произведениях искусства, но и основой красоты, источником эстетического удовлетворения.

Вот конкретный пример. На знаменитой картине И. И. Шишкина «Сосновая роща» с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны — освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали. Слева от главной сосны находится множество сосен — при желании можно с успехом продолжить деление картины по золотому сечению и дальше.

Наличие в картине ярких вертикалей и горизонталей, делящих ее в отношении золотого сечения, придает ей характер уравновешенности и спокойствия, в соответствии с замыслом художника. Когда же замысел художника иной, если, скажем, он создает картину с бурно развивающимся действием, подобная геометрическая схема композиции (с преобладанием вертикалей и горизонталей) становится неприемлемой.

Шедевром красоты считается Афродита Милосская, созданная Агесандром.

Ведущий: Уже кажется, что нет такой сферы человеческой деятельности, где бы не нашло себе место золотое сечение. Масштабы его присутствия поистине поражают воображение, однако, к сожалению, мы его очень часто не видим, а не видим, потому что даже и не подразумеваем о его существовании.

Свежие документы: Конспект урока по биологии в 10 классе«Строение и химический состав клетки»

Фома: Теперь мне все понятно… Хотя, нет. Я не могу понять: как же такие неразумные существа как моллюски смогли определить и избрать для себя идеальную форму роста и существования в виде спиральной раковины? Могли ли эти живые существа, которых ученых мир называет примитивными формами жизни, рассчитать, что идеальной для их существования будет логарифмическая форма ракушки?

Креационист: Конечно же нет, потому что такой замысел невозможно осуществить без наличия разума и знаний. Но таковым разумом не обладают ни примитивные моллюски, ни бессознательная природа, которую, правда, некоторые ученые называют создательницей жизни на земле. Пытаться объяснить происхождение подобной даже самой примитивной формы жизни случайным стечением неких природных обстоятельств по меньшей мере абсурдно. Совершенно ясно, что этот проект является осознанным творением. По этому закону Великого Божественного Творения созданы галактики, сотворены растения и микроорганизмы, тело человека, кристаллы, живые существа, молекула ДНК и законы физики, тогда как ученые и люди искусства лишь изучают этот закон и стараются подражать ему, воплощать этот закон в своих творениях.

Вне сомнения, что все в нашем мире, в окружающей нас жизни сотворено Всевышним Господом без какого либо подобия. Тогда как люди только копируют и подражают примерам, существующим в природе, которые Он сотворил.

Можно сказать, что эстетически правильные формы в строении живых существ, к которым, в частности, относится и пропорция золотое сечение — абсолютно бесполезны в плане повышения жизнеспособности организмов.

Ботаник: В самом деле, зачем, к примеру, злаковым растениям нужен стебель, разбитый на отдельные колена, соотношение длин между которыми тяготеет к золотой пропорции? Такое деление стебля нисколько не повышает его прочность и абсолютно бесполезно с точки зрения повышения возможностей выживания вида. И, тем не менее, это явление широко встречается у злаков.

Зоолог: У стрекоз общая длина тела и его частей — хвоста и корпуса, также связаны между собой пропорцией золотое сечение, хотя это никак не повышает их летательную способность.

Анатом: У человека с золотой пропорцией связан целый ряд морфологических структур его тела, хотя это нисколько не повышает способности брать предметы.

Креационист: Таких примеров можно привести довольно много. Все они, по большому счету, указывают на несостоятельность дарвиновской концепции видообразования. Ведь если бы в основе механизма образования биологического вида лежал естественный отбор,- способность выживать наиболее приспособленных к условиям обитания особей, — то откуда бы тогда в природе появилось множество абсолютно бесполезных в плане выживания эстетически-организованных структур.

Дарвинизм, как известно, в последние годы столкнулся с целым комплексом проблем, по-видимому, совершенно неразрешимых для него. В научной среде все более и более популярными становятся креационные идеи, согласно которым наш мир во всей его сложности и многообразии появился не в результате каких-то случайных процессов, но является продуктом Божественного Сотворения. С креационной точки зрения эстетически правильные структуры в природе — вещь вполне закономерная, свидетельствующая о Божественной благости и премудрости, раскрывающимися через творение.

Бог сотворил наш мир, отпечатлев в структуре природы символическое отображение «надмирного мира» — золотую пропорцию. Человек, как образ Божий, в своем художественном творчестве способен неосознанно повторять это же отображение, в следствии чего золотая пропорция проявляется и в структуре художественных произведений.

Ведущий: Спасибо. На этот вопрос существует и другая точка зрения.

Физик: Да. Я думаю, что существование Золотого сечения вполне объяснимо с точки зрения выгоды для живых организмов. Следует вспомнить, что феномен экономии энергии давно привлекает внимание механиков и физиков. С минимальным расходом энергии связаны известные в механике и физике принципы Мопертьюи, Остроградского-Гаусса, Гамильтона. Золотое сечение и числа Фибоначчи представляют своего рода «технологический рецепт» оптимизации живых структур и организмов, связанный с экономией энергии. Несомненно, что природа избрала золотое сечение как один из «способов» оптимального сопряжения систем как живой, так и неживой природы. Оптимизация конструкции позволяет каждому организму адекватно исполнять свою функцию при минимально возможном расходе ресурсов внешней среды.

Ведущий: Ну что же, пусть каждый сам для себя решит, какая гипотеза о происхождении Золотого сечения. Но то, что она существует- это неоспоримый факт. Мы убедились в том, что все в природе подчинено единому плану, единым законам — и раскрыть и объяснить эти законы и есть главная задача человеческой науки.

А сейчас проведем небольшую викторину по данной теме:

Вопросы викторины:

Что такое Золотое сечение? (Золото́е сече́ние— деление отрезка на части в таком соотношении, при котором меньшая часть относится к большей, как большая ко всему в целом).

Чему равно число Ф? (1.61803398875)

3. Приведите примеры проявления Золотой пропорции у растений. (Например, явление «филлотаксиса». Спирально закручиваются усики растений, по спирали происходит рост тканей в стволах деревьев, по спирали расположены семечки в подсолнечнике, спиральные движения (нутации) наблюдаются при росте корней и побегов. Пяти- лепестковыми являются цветы кувшинки, шиповника, боярышника, гвоздики, груши, черемухи, яблони, земляники и многих других, расположение листьев на стеблях).

4. Приведите примеры проявления Золотой пропорции у животных. (Членение «по Фибоначчи» весьма распространено среди различных типов животных, включая членистоногих, насекомых, черепах и высших животных. Тело членистоногих состоит из трех отделов: головной, грудной и брюшной. Для всего животного мира характерны симметрия форм и наличие парных органов, членение на три части тела (голова, грудь, брюшко), членение конечностей на 3 и 5 частей, а брюшка — на 3. Это является характерной чертой морфологии насекомых.

У черепахи в панцире имеется 13 сросшихся роговых пластин, из них 5 пластин в центре, а 8 по краям, на лапках 5 пальцев, а позвоночник содержит 34 позвонка. У гавиалового крокодила Малайского архипелага вдоль туловища расположены 55 роговых пластин. На теле кавказской носатой гадюки также 55 темных пятен, а в скелете габонской гадюки насчитали 144 позвонка. У млекопитающих — число костей скелета в различных частях тела у самых разнообразных животных близко к 13 (кит, верблюд, олень, тур и т.д.), число позвонков близко к 34 и 55. У некоторых моллюсков количество частей, формирующих конические раковины, отвечает числам Фибоначчи).

5. Приведите примеры проявления Золотой пропорции в строении тела человека. (У человека одно туловище, одна голова, одно сердце и т. д.; многие части тела и органы парные, например, руки, ноги, глаза, почки. Из трех частей состоят ноги, руки, пальцы рук. На руках и ногах по пять пальцев, а рука вместе с пальцами состоит из восьми частей. У человека 12 пар ребер (одна пара атрофирована и присутствует в виде рудимента). Очевидно, в прошлом у человека было 13 пар ребер, но в процессе эволюции, при переходе к прямостоячему положению количество ребер уменьшилось. Число молочных зубов у ребенка равно 20, а у взрослого достигает 32, причем последняя пара («зубы мудрости») появляется позже других и не у всех людей. Общее число костей скелета человека близко к 233. В строении головного мозга различают семь частей. В основании головного мозга выделяют 8 частей, выполняющих разные функции. В теле человека насчитывается 8 различных желез внутренней секреции. Кишечник и соседние с ним органы (желудок, печень, желчный пузырь и т.д.) составляют в сумме 13 органов. Дыхательные органы человека состоят из 8 частей. Печень также состоит из 8 частей; почки состоят из 5 частей, а сердце из 13.

В теле человека насчитывают около 630 мышц, составляющих около 0,4 массы тела человека.

На человеческом лице существуют и иные воплощения правила золотого сечения. Вот несколько таких соотношений:
Высота лица / ширина лица,
Центральная точка соединения губ до основания носа / длина носа.
Высота лица / расстояние от кончика подбородка до центральной точки соединения губ
Ширина рта / ширина носа,
Ширина носа / расстояние между ноздрями,
Расстояние между зрачками / расстояние между бровями).

6. В каких еще науках можно найти закономерности, присущие Золотой пропорции? (Практически во всех науках и отраслях деятельности человека: в Биологии, химии, физике, в искусстве, математике и т.д.)

7. Как можно объяснить то, что Золотые пропорции встречаются в творениях человека? (Пропорции Золотого сечения являются основой красоты, источником эстетического удовлетворения).

8. Как вы думаете, почему строение живых организмов подчинено закону Золотого сечения? (Существование Золотого сечения вполне объяснимо с точки зрения выгоды для живых организмов. Золотое сечение и числа Фибоначчи представляют своего рода «технологический рецепт» оптимизации живых структур и организмов, связанный с экономией энергии. Несомненно, что природа избрала золотое сечение как один из «способов» оптимального сопряжения систем как живой, так и неживой природы. Оптимизация конструкции позволяет каждому организму адекватно исполнять свою функцию при минимально возможном расходе ресурсов внешней среды).