Материалы к уроку – практикум
по решению стереометрических задач или
«История развития одной задачи».
Учитель ГОУ СОШ № 250: Муковнина Людмила Михайловна
Задача 1: (№161 учебник «Геометрия 10-11» Л. С. Атанасян)
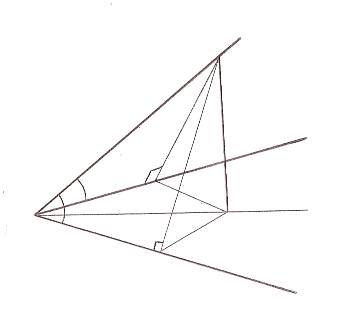
Луч ВА не лежит в плоскости неразвернутого угла CBD. Докажите, что если ![]() , причём
, причём ![]() < 90º, то проекцией луча ВА на плоскость CBD является биссектриса угла CBD.
< 90º, то проекцией луча ВА на плоскость CBD является биссектриса угла CBD.
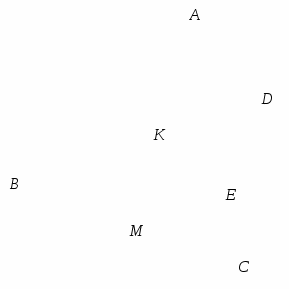
Решение:
1). Пусть ![]() . В плоскости АВС проведём перпендикуляр АМ к прямой ВС, а в плоскости ABD – перпендикуляр АК к прямой BD. Так как
. В плоскости АВС проведём перпендикуляр АМ к прямой ВС, а в плоскости ABD – перпендикуляр АК к прямой BD. Так как ![]() < 90º, то точка М лежит на луче ВС (а не на продолжении этого луча). Аналогично, так как
< 90º, то точка М лежит на луче ВС (а не на продолжении этого луча). Аналогично, так как ![]() < 90º, то точка К лежит на луче BD.
< 90º, то точка К лежит на луче BD.
Так как ![]() , то
, то ![]() (по теореме, обратной теореме о трёх перпендикулярах). Аналогично доказывается, что
(по теореме, обратной теореме о трёх перпендикулярах). Аналогично доказывается, что ![]() .
.
2). Прямоугольные треугольники АВК и АВМ равны по гипотенузе (АВ – общая гипотенуза) и острому углу (![]() ), следовательно, ВМ = ВК.
), следовательно, ВМ = ВК.
3). Прямоугольные треугольники ВМЕ и ВКЕ равны по гипотенузе (ВЕ – общая гипотенуза) и катету (ВМ = ВК), следовательно, ЕМ = ЕК.
4). Точка Е равноудалена от сторон угла CBD, следовательно, она лежит на биссектрисе этого угла, т. е. луч ВЕ – биссектриса угла CBD, что и т. д.
Задача 2: Основание призмы – правильный треугольник АВС. Боковое ребро ![]() образует равные острые углы со сторонами основания АВ и АС.
образует равные острые углы со сторонами основания АВ и АС.
Докажите, что: а) ![]() ; б) грань
; б) грань ![]() – прямоугольник.
– прямоугольник.
О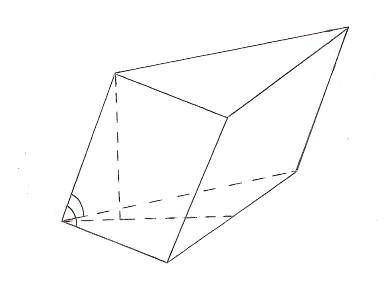

Решение:
а) Так как ![]() образует равные углы со сторонами АВ и АС, то проекцией ребра
образует равные углы со сторонами АВ и АС, то проекцией ребра ![]() на плоскость АВС является отрезок АО биссектрисы угла ВАС.
на плоскость АВС является отрезок АО биссектрисы угла ВАС. ![]() , следовательно,
, следовательно, ![]() по теореме о трёх перпендикулярах.
по теореме о трёх перпендикулярах.
б) ![]() ,
, ![]() ||
|| ![]() , поэтому
, поэтому ![]() , следовательно
, следовательно ![]() – прямоугольник, что и т. д.
– прямоугольник, что и т. д.
Задача 3: Все грани призмы ![]() – равные ромбы со стороной, равной a. Углы
– равные ромбы со стороной, равной a. Углы ![]() ,
, ![]() и
и ![]() равны 60º каждый. Найдите угол между прямой
равны 60º каждый. Найдите угол между прямой ![]() и плоскостью
и плоскостью ![]() .
.
Решение:
Первый способ:
А А1 C1 D1 H H1 B C D B1 K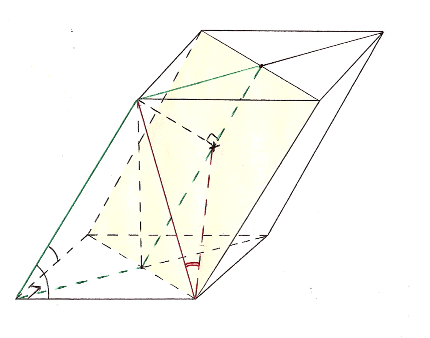
1) Не трудно доказать, что ![]() – прямоугольник.
– прямоугольник.
2) Так как все грани призмы ![]() – равные ромбы и углы
– равные ромбы и углы ![]() ,
, ![]() и
и ![]() равны 60º каждый, то
равны 60º каждый, то ![]() , таким образом
, таким образом ![]() и точка Н – центр описанной окружности около треугольника ABD, т. е. середина BD.
и точка Н – центр описанной окружности около треугольника ABD, т. е. середина BD.
3) 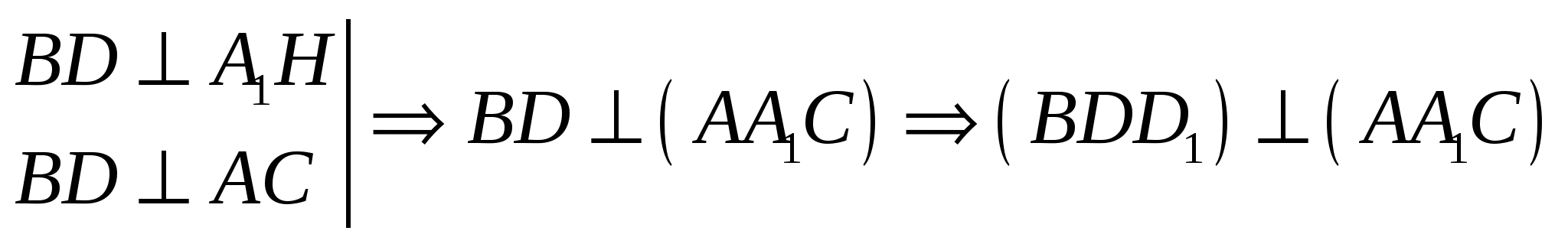 и
и ![]() по прямой
по прямой ![]() , тогда
, тогда ![]() и
и ![]() .
.
4) ![]() – параллелограмм,
– параллелограмм, ![]()
![]()
![]()
![]()
![]()
5) ![]() – угол между прямой
– угол между прямой ![]() и плоскостью
и плоскостью ![]() ,
, ![]() ,
, ![]() ; таким образом
; таким образом ![]() .
.
Ответ: 30º.
В D1 C1
А1 В1 А B C D K a a a α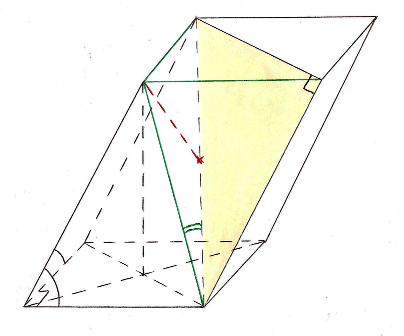
![]() – пирамида,
– пирамида, ![]() основанию пирамиды, боковые рёбра равны
основанию пирамиды, боковые рёбра равны ![]() , отсюда К – центр описанной окружности.
, отсюда К – центр описанной окружности.
![]() ,
, ![]() , по теореме Пифагора
, по теореме Пифагора ![]() ,
, ![]() . Из треугольника
. Из треугольника ![]()
![]() , следовательно
, следовательно ![]() .
.
Ответ: 30º.
4
