Конспект урока по математике «Формулы квадрата суммы и квадрата разности двух выражений» 7 класс

Как умножить многочлен на многочлен?

3. Изучение нового материала.

Квадрат суммы двух выражений. Умножение многочлена на многочлен в некоторых случаях удается выполнить короче. Равенства, выражающие эти частные случаи умножения, называются формулами сокращенного умножения.

Возведем в квадрат сумму двух выражений а и b:

(а+b)²=(a+b)(a+b)=a²+ab+ab+b²

т.е. мы доказали справедливость тождества:

(а+b)² =a²+2ab+b² (1)

Тождество (1) называют формулой квадрата суммы двух выражений. Отсюда получим правило:

Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.

Квадрат разности двух выражений. Теперь возведем в квадрат разность а-b

(а-b)²=(a-b)(a-b)=a²-ab-ab+b²= a²-2ab+b²

Значит,

(а-b)²= a²-2ab+b² (2)

Квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.

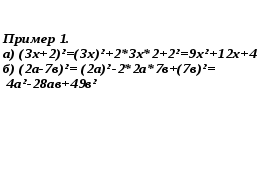
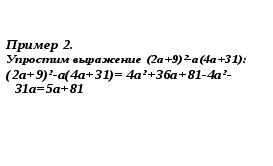
С помощью формул (1) и (2) удобно вычислять квадраты чисел, на несколько едениц отличающихся от «круглого» числа.

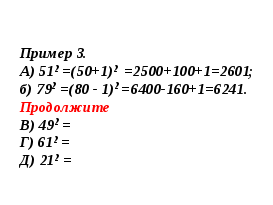
Формулы (1) и (2) часто используются и в обратном порядке, т.е. в виде:

a²+2ab+b² = (а+b)²

a²-2ab+b² = (а-b)²

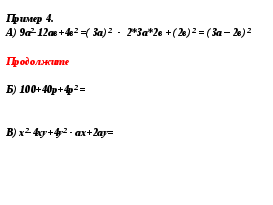
3. Закрепление нового материала:

4. Контрольные вопросы

— Напишите формулу квадрата суммы и дайте ее формулировку словами.

— Напишите формулу квадрата разности и дайте ее формулировку словами.

5.Задание на дом: §1, №332(1,3,5,7,9), 338(2,4,6)

6. Подведение итогов урока

Проводится с помощью кубика- экзаменатора, на каждой грани которого записан номер примера. Вызванный к доске ученик подбрасывает кубик и комментирует выпавшую ему на верхней грани часть формулы. Записывает это на доске вместе с многочленом, в который можно преобразовать данный квадрат двучлена Задания для кубика – экзаменатора