























 Муниципальное бюджетное общеобразовательное учреждение
Муниципальное бюджетное общеобразовательное учреждение
«Вечерняя сменная средняя общеобразовательная школа при ИУ»
Конспект урока
Метод координат на плоскости.
Координаты на прямой
подготовила
учитель математики
Щукина Татьяна Викторовна
. Калининград
2012
Метод координат на плоскости.
Координаты на прямой
Цель: подготовить учащихся к изучению тем «Векторы», «Метод координат»
Задачи:
повторить тему «Координаты на прямой»;
отработка навыков работы с формулами;
3) повышение математической культуры;
4) привитие интереса к математике.
Оборудование: ноутбук, мультимедийный проектор, экран
Межпредметные связи
Алгебра: «Рациональные числа», «Алгебраические выражения»
География: «Географические координаты»
Физика: график изотермы
Структура урока
Подготовка к восприятию изучаемого материала. Исторические сведения.
Изучение нового материала
Метод координат на плоскости
Координаты на прямой
Закрепление изученного. Решение задач.
Рефлексия.
Ход урока
Подготовка к восприятию изучаемого материала. Исторические сведения.
Сегодня мы с вами начнём изучать очень важную тему математики «Метод координат».
Слайд 2
Основоположником метода координат принято считать французского математика и философа Рене Декарта. Он родился 31 марта 1596 года в небольшом французском городе Лаэ. Работа, в которой изложены основные идеи координатного метода, была опубликована Декартом в 1637 году в приложении «Геометрия» к его книге «Рассуждения о методе».
Декарт первый стал обозначать неизвестные величины через 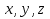 и т.д. Идеи Декарта оказали большое влияние на развитие математики в последующие два столетия.
и т.д. Идеи Декарта оказали большое влияние на развитие математики в последующие два столетия.
«Метод координат на плоскости»
5 января 1969 года в 14 часов дня было передано по радио сообщение ТАСС об осуществлении в советском Союзе запуска автоматической межпланетной станции «Венера-5».
В сообщении, кроме характеристики станции и целей её запуска, сказано:
Слайд 3
Слайд 4
Можно ли по этим данным определить, над территорией какого государства находилась станция? Назовите это государство (Юго-Восточный Китай).
Что же такое координаты?
Мореплаватели, лётчики, путешественники, геологи, военные и т.д. для определения своего местонахождения пользуются координатами, т.е. числами, которые указывают положение какой-либо точки на местности. Эти числа отсчитываются в определённой системе координат — в данном случае в географической системе координат. Эта система нанесена в виде параллелей и меридианов на карте.
Координатами пользуются метеорологи при снятии показателей самопишущих приборов — термографов (время суток и температура), барографов (время суток и атмосферное давление) и т.д. здесь координатами тоже являются числа: время суток, температура, величина атмосферного давления. В этом случае числа тоже отсчитываются в определённой системе координат — линий на специальной ленте для самопишущего прибора.
Слайд 5
В городах все улицы имеют названия, а все дома и квартиры в них занумерованы. По адресу, состоящему из названия улицы, номера дома и номера квартиры, доставляется почта. Если вместо названия улицы использовать номера (например, 23-я улица), то адрес можно будет записать тремя числами: 23/19/8. Эти числа можно назвать координатами квартиры.
Примеров использования координат очень много.
Так что же такое «координаты»?
Координаты — это числа, выбираемые в определённом порядке и позволяющие в выбранной системе координат находить положение объекта.
В математике система координат имеет исключительно важное значение. Она позволяет геометрические свойства фигур переводить на язык алгебры и, наоборот, алгебраические вопросы интерпретировать геометрически.
Для того чтобы мы могли на практике применять метод координат давайте вспомним основные в этой теме определения. Что такое:
координатная ось;
координата;
система координат.
Координаты на прямой
Положение точки на прямой может быть единственным образом охарактеризовано числом. Для этого выберем на заданной прямой произвольную точку О.
Слайд 6
Она делит прямую на две полупрямые. Одну из них условно назовём положительной (движение вправо от точки О) и отметим это стрелкой (ЩЛКМ), другую отрицательной (движение влево от точки О). На положительной полупрямой выберем точку Е (ЩЛКМ). Отрезок ОЕ примем за единицу измерения. Поставим в соответствие точке О — число нуль, а точке Е — число 1 (ЩЛКМ).
Определение
Прямая, на которой выбрано положительное направление, указаны начальная точка и единица измерения, называется координатной осью, или осью координат.
(ЩЛКМ) Возьмём теперь на положительной части координатной оси точку А. Её положение на оси можно охарактеризовать положительным числом 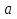 , равным длине отрезка ОА. Положение точки В, расположенной на отрицательной части оси, можно охарактеризовать отрицательным числом
, равным длине отрезка ОА. Положение точки В, расположенной на отрицательной части оси, можно охарактеризовать отрицательным числом 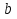 , абсолютная величина которого равна длине отрезка ОВ.
, абсолютная величина которого равна длине отрезка ОВ.
Определение
Число, которое характеризует положение точки на координатной оси, называется координатой этой точки.
Соответствие точки её координате записывается следующим образом: (ЩЛКМ).
Закрепление изученного материала. Решение задач
Слайд 7
Запишите координаты, изображённых на координатной оси точек.
Проверка (ЩЛКМ).
Постройте на координатной оси точки Р(-4), В(2), О(0)
Проверка (ЩЛКМ).
Итак, вывод: если дана координата какой-либо точки, то мы всегда можем найти на координатной оси единственную точку и, наоборот, если дана какая-либо точка М на оси, то мы всегда можем найти её координату.
Это означает, что между числами и точками координатной оси можно установить взаимно однозначное соответствие.
Задачи (упражнения для закрепления)
Отметить на координатной оси точки: А(3), В(-2), С(3,5), D(0,7), Е(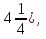 К(
К( ), L(-1).
), L(-1).
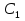
 (рис.1). Запишите их координаты.
(рис.1). Запишите их координаты.
Рис.1 x 1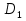

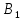
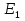
3. Числа 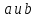 заданы точками А и В на координатной оси (рис.2). вычислить числа
заданы точками А и В на координатной оси (рис.2). вычислить числа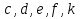 по формулам:
по формулам:
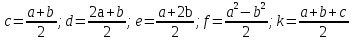
Рис.2 B 20 15 A 10 x
Отметить на оси точки 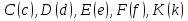 .
.
Даны три числа: 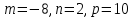 . На координатной оси найти точки
. На координатной оси найти точки 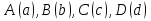 , координаты которых вычислить по формулам:
, координаты которых вычислить по формулам: 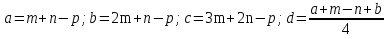 . Отметить на оси точки
. Отметить на оси точки 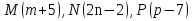 .
.
Рефлексия.
Преподаватель: Подведем итоги нашего урока.
1) Что интересного вы узнали о методе координат на сегодняшнем уроке?
2) применяется ли метод координат в реальной жизни? Приведите примеры.
3) Выразите свои впечатления об уроке одним предложением.
Список литературы
Методический сборник «В помощь учителю математики» (статья И.Б. Гольдберга «Метод координат», стр.37 — 95), Калининград, Кн. Изд., 1971г.
https://aphorism-list.com/autors.php?page=dekart&tkautors=dekart
Картинки
CD «Портреты великих учёных», наглядные пособия, изд. «Учитель»
https://www.egetutor.ru/TestBase/Matematika/Opredelenie-i-grafik-funkcii.aspx
7
