Подготовила: учитель математики
Категория: первая
Быстролетова Татьяна Дмитриевна
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №1 им. Ляпидевского
Станица Старощербиновская Щербиновского района Краснодарского края
Подготовка к ГИА.
Площади фигур.
2014 г.
Для учителей выпускных классов наиболее важным завершением учебного года являются экзамены девятиклассников и одиннадцатиклассников – ЕГЭ и ГИА. Всем очень хочется подготовить своих выпускников так, чтобы они сдали экзамены на максимальный балл. В интернете огромное количество сайтов предлагающих те или иные методы подготовки, огромнейшее количество литературы, но ничто и никто не поможет нашим детям сдать экзамен хорошо, чем мы сами. Представленная работа может помочь учителю в обобщении и систематизации знаний по теме «Площади фигур», ее можно использовать на любом этапе урока. Понятие площади и её свойств изучаются с опорой на наглядные представления обучающихся и их жизненный опыт. Вычисление площадей многоугольников и круга является составной частью решения задач на многогранники и тела вращения в курсе стереометрии. Поэтому при изучении данной темы основное внимание необходимо уделять формированию самого представления площади и формированию практических навыков вычисления площадей плоских фигур в ходе решения соответствующих задач. Поэтому данный материал направлен на закрепление и повторения умений решать задачи на нахождение площадей фигур.
Данная работа состоит из 1 части (работа в классе ) и подробного разбора заданий.
Работа в классе
1. B 8 № 39. 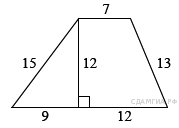 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
2. B 8 № 65. 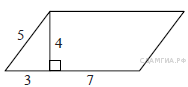 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
3. B 8 № 91. Найдите площадь параллелограмма, изображённого на рисунке.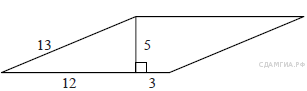
4. B 8 № 117. 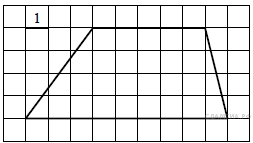 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
5. B 8 № 143. 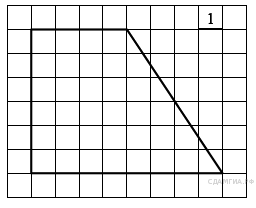 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
6. B 8 № 195. 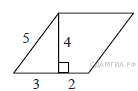 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
7. B 8 № 169839. В прямоугольном треугольнике один из катетов равен 10, а острый угол, прилежащий к нему, равен ![]() . Найдите площадь треугольника.
. Найдите площадь треугольника.
8. B 8 № 169840. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.
9. B 8 № 169841. В прямоугольном треугольнике один из катетов равен 10, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
10. B 8 № 169842. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен ![]() . Найдите площадь треугольника.
. Найдите площадь треугольника.
11. B 8 № 169847. Сторона равностороннего треугольника равна 10. Найдите его площадь,делённую на ![]() .
.
12. B 8 № 169848. Периметр равностороннего треугольника равен 30. Найдите его площадь,делённую на ![]() .
.
13. B 8 № 169849. Высота равностороннего треугольника равна 10. Найдите его площадь,делённую на ![]()
14. B 8 № 169850. В равнобедренном треугольнике боковая сторона равна 10, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, делённую на ![]()
15. B 8 № 169851. Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.
16. B 8 № 169852. Периметр равнобедренного треугольника равен 16, а основание — 6. Найдите площадь треугольника.
17. B 8 № 169853. В треугольнике одна из сторон равна 10, а опущенная на нее высота — 5. Найдите площадь треугольника.
18. B 8 № 169854. В треугольнике одна из сторон равна 10, другая равна ![]() , а угол между ними равен 60°. Найдите площадь треугольника.
, а угол между ними равен 60°. Найдите площадь треугольника.
19. B 8 № 169855. В треугольнике одна из сторон равна 10, другая равна ![]() , а угол между ними равен 45°. Найдите площадь треугольника.
, а угол между ними равен 45°. Найдите площадь треугольника.
20. B 8 № 169856. В треугольнике одна из сторон равна 10, другая равна ![]() , а угол между ними равен 120°. Найдите площадь треугольника.
, а угол между ними равен 120°. Найдите площадь треугольника.
21. B 8 № 169857. В треугольнике одна из сторон равна 10, другая равна ![]() , а угол между ними равен 135°. Найдите площадь треугольника.
, а угол между ними равен 135°. Найдите площадь треугольника.
22. B 8 № 169858. В треугольнике одна из сторон равна 10, другая равна 12, а угол между ними равен 30°. Найдите площадь треугольника.
23. B 8 № 169859. В треугольнике одна из сторон равна 12, другая равна 16, а синус угла между ними равен ![]() . Найдите площадь треугольника.
. Найдите площадь треугольника.
24. B 8 № 169860. В треугольнике одна из сторон равна 12, другая равна 10, а косинус угла между ними равен ![]() . Найдите площадь треугольника.
. Найдите площадь треугольника.
25. B 8 № 169862. Сторона квадрата равна 10. Найдите его площадь.
26. B 8 № 169863. Периметр квадрата равен 40. Найдите площадь квадрата.
27. B 8 № 169864. В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
28. B 8 № 169865. В прямоугольнике одна сторона равна 10, периметр равен 44. Найдите площадь прямоугольника.
29. B 8 № 169866. В прямоугольнике одна сторона равна 6, а диагональ равна 10. Найдите площадь прямоугольника.
30. B 8 № 169867. В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 30°. Найдите площадь прямоугольника, делённую на ![]() .
.
31. B 8 № 169868. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
32. B 8 № 169869. Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.
33. B 8 № 169870. Периметр ромба равен 40, а один из углов равен 45°. Найдите площадь ромба,делённую на ![]() .
.
34. B 8 № 169871. Периметр ромба равен 40, а один из углов равен 60°. Найдите площадь ромба,делённую на ![]() .
.
35. B 8 № 169872. Периметр ромба равен 24, а синус одного из углов равен ![]() . Найдите площадь ромба.
. Найдите площадь ромба.
36. B 8 № 169873. Периметр ромба равен 24, а косинус одного из углов равен ![]() . Найдите площадь ромба.
. Найдите площадь ромба.
37. B 8 № 169874. Периметр ромба равен 24, а тангенс одного из углов равен ![]() . Найдите площадь ромба.
. Найдите площадь ромба.
38. B 8 № 169875. Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.
39. B 8 № 169876. Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на ![]() .
.
40. B 8 № 169877. Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 60°. Найдите площадь параллелограмма, делённую на ![]() .
.
41. B 8 № 169878. Одна из сторон параллелограмма равна 12, другая равна 5, а синус одного из углов равен ![]() . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
42. B 8 № 169879. Одна из сторон параллелограмма равна 12, другая равна 5, а косинус одного из углов равен ![]() . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
43. B 8 № 169880. Одна из сторон параллелограмма равна 12, другая равна 5, а тангенс одного из углов равен ![]() . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
44. B 8 № 169881. Основания трапеции равны 18 и 12, одна из боковых сторон равна ![]() , а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
, а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
45. B 8 № 169882. Основания трапеции равны 18 и 10, одна из боковых сторон равна ![]() , а угол между ней и одним из оснований равен 120°. Найдите площадь трапеции.
, а угол между ней и одним из оснований равен 120°. Найдите площадь трапеции.
46. B 8 № 169883. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а синус угла между ней и одним из оснований равен ![]() . Найдите площадь трапеции.
. Найдите площадь трапеции.
47. B 8 № 169884. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а косинус угла между ней и одним из оснований равен ![]() . Найдите площадь трапеции.
. Найдите площадь трапеции.
48. B 8 № 169885. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а тангенс угла между ней и одним из оснований равен ![]() . Найдите площадь трапеции.
. Найдите площадь трапеции.
49. B 8 № 169886. Радиус круга равен 1. Найдите его площадь, деленную на π.
50. B 8 № 169887. Найдите площадь кругового сектора, если радиус круга равен 3, а угол сектора равен 120°. В ответе укажите площадь, деленную на π.
51. B 8 № 169888. Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6π, а угол сектора равен 120°. В ответе укажите площадь, деленную на π.
52. B 8 № 169889. В прямоугольном треугольнике один из катетов равен 10, острый угол, прилежащий к нему, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на ![]() .
.
53. B 8 № 169890. В прямоугольном треугольнике один из катетов равен ![]() , острый угол, прилежащий к нему, равен 30°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на
, острый угол, прилежащий к нему, равен 30°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на ![]() .
.
54. B 8 № 169891. В прямоугольном треугольнике один из катетов равен 10, угол, лежащий напротив него, равен 30°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на ![]() .
.
55. B 8 № 169892. В прямоугольном треугольнике один из катетов равен ![]() , угол, лежащий напротив него, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на
, угол, лежащий напротив него, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на ![]() .
.
56. B 8 № 169893. В равнобедренном треугольнике боковая сторона равна 10, основание — ![]() , а угол, лежащий напротив основания, равен 30°. Найдите площадь треугольника.
, а угол, лежащий напротив основания, равен 30°. Найдите площадь треугольника.
57. B 8 № 169894. В равнобедренном треугольнике боковая сторона равна 10, основание — ![]() , а угол, лежащий напротив основания, равен 45°. Найдите площадь треугольника, деленную на
, а угол, лежащий напротив основания, равен 45°. Найдите площадь треугольника, деленную на ![]()
58. B 8 № 169895. В равнобедренном треугольнике боковая сторона равна 10, основание — ![]() , а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, деленную на
, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, деленную на ![]()
59. B 8 № 169896. В равнобедренном треугольнике боковая сторона равна 10, основание — ![]() , а угол, лежащий напротив основания, равен 135°. Найдите площадь треугольника, деленную на
, а угол, лежащий напротив основания, равен 135°. Найдите площадь треугольника, деленную на ![]()
60. B 8 № 169897. В равнобедренном треугольнике боковая сторона равна 10, основание — ![]() , а угол, лежащий напротив основания, равен 150°. Найдите площадь треугольника.
, а угол, лежащий напротив основания, равен 150°. Найдите площадь треугольника.
61. B 8 № 169898. В прямоугольнике диагональ равна 10, угол между ней и одной из сторон равен 30°, длина этой стороны ![]() . Найдите площадь прямоугольника, деленную на
. Найдите площадь прямоугольника, деленную на ![]()
62. B 8 № 169899. В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 60°, длина этой стороны равна 5. Найдите площадь прямоугольника, деленную на ![]()
63. B 8 № 169900. В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, лежащий напротив этой диагонали, равен 30°. Найдите площадь ромба.
, а угол, лежащий напротив этой диагонали, равен 30°. Найдите площадь ромба.
64. B 8 № 169901. В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, лежащий напротив этой диагонали, равен 45°. Найдите площадь ромба, деленную на
, а угол, лежащий напротив этой диагонали, равен 45°. Найдите площадь ромба, деленную на ![]()
65. B 8 № 169902. В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, лежащий напротив этой диагонали, равен 120°. Найдите площадь ромба, деленную на
, а угол, лежащий напротив этой диагонали, равен 120°. Найдите площадь ромба, деленную на ![]()
66. B 8 № 169903. В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, лежащий напротив этой диагонали, равен 135°. Найдите площадь ромба, деленную на
, а угол, лежащий напротив этой диагонали, равен 135°. Найдите площадь ромба, деленную на ![]()
67. B 8 № 169904. В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, лежащий напротив этой диагонали, равен 150°. Найдите площадь ромба.
, а угол, лежащий напротив этой диагонали, равен 150°. Найдите площадь ромба.
68. B 8 № 169905. В ромбе сторона равна 10, одна из диагоналей — 10, а угол, лежащий напротив этой диагонали, равен 60°. Найдите площадь ромба, деленную на ![]()
69. B 8 № 169906. В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, из которого выходит эта диагональ, равен 150°. Найдите площадь ромба.
, а угол, из которого выходит эта диагональ, равен 150°. Найдите площадь ромба.
70. B 8 № 169908. В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, из которого выходит эта диагональ, равен 60°. Найдите площадь ромба, деленную на
, а угол, из которого выходит эта диагональ, равен 60°. Найдите площадь ромба, деленную на ![]()
71. B 8 № 169909. В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, из которого выходит эта диагональ, равен 45°. Найдите площадь ромба, деленную на
, а угол, из которого выходит эта диагональ, равен 45°. Найдите площадь ромба, деленную на ![]()
72. B 8 № 169910. В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, из которого выходит эта диагональ, равен 30°. Найдите площадь ромба.
, а угол, из которого выходит эта диагональ, равен 30°. Найдите площадь ромба.
73. B 8 № 169911. В ромбе сторона равна 10, одна из диагоналей — 10, а угол, из которого выходит эта диагональ, равен 120°. Найдите площадь ромба, деленную на ![]()
74. B 8 № 169912. Радиус круга равен 3, а длина ограничивающей его окружности равна 6π. Найдите площадь круга. В ответ запишите площадь, деленную на π.
75. B 8 № 169913. Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6π, угол сектора равен 120°, а радиус круга равен 9. В ответ укажите число, деленную на π.
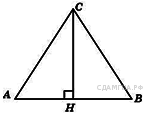
76. B 8 № 311332. В равнобедренном треугольнике ![]() . Найдите
. Найдите ![]() , если высота
, если высота ![]() .
.
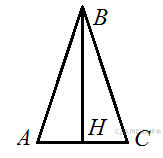
77. B 8 № 311375. В равнобедренном треугольнике ![]() . Найдите
. Найдите ![]() , если высота
, если высота ![]() .
.
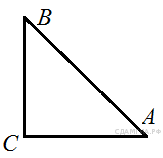
78. B 8 № 311387. В треугольнике ![]() угол
угол ![]() равен 90°,
равен 90°, ![]() . Найдите
. Найдите ![]() .
.
79. B 8 № 311399. В треугольнике ![]() угол
угол ![]() равен 90°,
равен 90°, ![]() . Найдите
. Найдите ![]() .
.
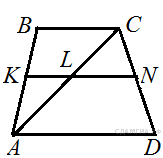
80. B 8 № 311411. Основания трапеции равны 4 см и 10 см. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.
81. B 8 № 311475. Диагональ трапеции делит её среднюю линию на отрезки, равные 4 см и 3 см. Найдите меньшее основание трапеции.
82. B 8 № 311480. Средняя линия трапеции равна 11, а меньше основание равно 5. Найдите большее основание трапеции.
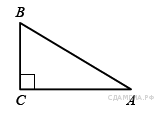
83. B 8 № 311498. В треугольнике ![]() угол
угол ![]() прямой,
прямой, ![]() . Найдите
. Найдите ![]() .
.
84. B 8 № 311500. 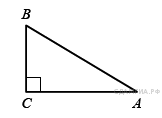 В треугольнике
В треугольнике ![]() угол
угол ![]() прямой,
прямой, ![]() . Найдите
. Найдите ![]() .
.
85. B 8 № 311682.  Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
86. B 8 № 311761. Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой.
87. B 8 № 311849. Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.
88. B 8 № 311913. 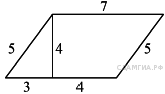 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
89. B 8 № 311957.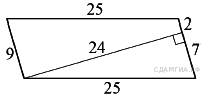
Найдите площадь параллелограмма, изображённого на рисунке.
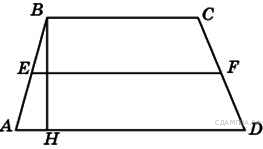
90. B 8 № 314870. 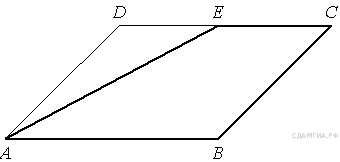 Площадь параллелограмма ABCD равна 56. Точка E — середина стороны CD. Найдите площадь трапецииAECB.
Площадь параллелограмма ABCD равна 56. Точка E — середина стороны CD. Найдите площадь трапецииAECB.
91. B 8 № 314876. 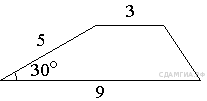 Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
92. B 8 № 314882. 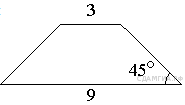 В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
93. B 8 № 315000. 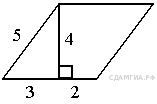 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
94. B 8 № 315074. 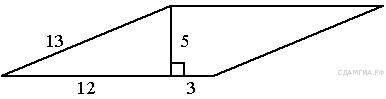 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
95. B 8 № 315084. 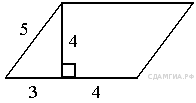 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
96. B 8 № 316231. Найдите площадь прямоугольника, если его периметр равен 92, а отношение соседних сторон равно 3:20.
97. B 8 № 316258. Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.
98. B 8 № 316284. Найдите площадь прямоугольника, если его периметр равен 102, а отношение соседних сторон равно 2:15.
99. B 8 № 316321. Найдите площадь прямоугольника, если его периметр равен 58 и одна сторона на 5 больше другой.
100. B 8 № 316347. 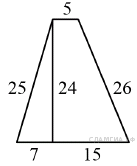 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
101. B 8 № 316373. 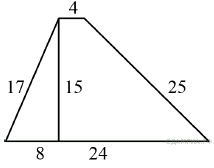 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
102. B 8 № 322861. 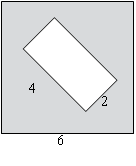 Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
103. B 8 № 323159. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
104. B 8 № 323179. ![]() Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
105. B 8 № 323282. В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
106. B 8 № 323285. В прямоугольном треугольнике один из катетов равен 35, а угол, лежащий напротив него равен 45∘. Найдите площадь треугольника.
107. B 8 № 323297.
В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него равен 45∘. Найдите площадь треугольника.
108. B 8 № 323356. 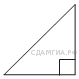 В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
109. B 8 № 323396. 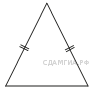 Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
110. B 8 № 323416. Периметр равнобедренного треугольника равен 196, а основание — 96. Найдите площадь треугольника.
111. B 8 № 323430.
Периметр равнобедренного треугольника равен 392, а основание – 192. Найдите площадь треугольника.
112. B 8 № 323436.  Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
113. B 8 № 323902. 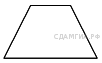 Основания равнобедренной трапеции равны 5 и 17, а ее боковые стороны равны 10. Найдите площадь трапеции.
Основания равнобедренной трапеции равны 5 и 17, а ее боковые стороны равны 10. Найдите площадь трапеции.
114. B 8 № 323957. 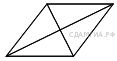 Найдите площадь ромба, если его диагонали равны 14 и 6.
Найдите площадь ромба, если его диагонали равны 14 и 6.
115. B 8 № 323977.  Периметр квадрата равен 160. Найдите площадь квадрата.
Периметр квадрата равен 160. Найдите площадь квадрата.
116. B 8 № 323997.  Найдите площадь квадрата, если его диагональ равна 1.
Найдите площадь квадрата, если его диагональ равна 1.
117. B 8 № 324017. 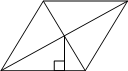 Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
118. B 8 № 324077. 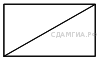 В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
119. B 8 № 324097.  Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.
Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.
120. B 8 № 324117. 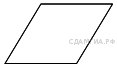 Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба.
Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба.
121. B 8 № 324155. 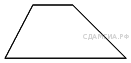 Основания трапеции равны 7 и 49, одна из боковых сторон равна 18 , а косинус угла между ней и одним из оснований равен
Основания трапеции равны 7 и 49, одна из боковых сторон равна 18 , а косинус угла между ней и одним из оснований равен ![]() Найдите площадь трапеции.
Найдите площадь трапеции.
122. B 8 № 324364.  Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
123. B 8 № 339837. 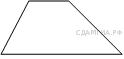 Основания трапеции равны 1 и 13, одна из боковых сторон равна 152√, а угол между ней и одним из оснований равен 135∘. Найдите площадь трапеции.
Основания трапеции равны 1 и 13, одна из боковых сторон равна 152√, а угол между ней и одним из оснований равен 135∘. Найдите площадь трапеции.
124. B 8 № 339859. 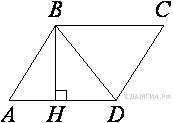 Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1 и HD = 28. Диагональ параллелограммаBD равна 53. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1 и HD = 28. Диагональ параллелограммаBD равна 53. Найдите площадь параллелограмма.
125. B 8 № 340197. 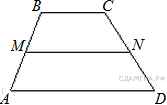 В трапеции ABCD AD = 5, BC = 2, а её площадь равна 28. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
В трапеции ABCD AD = 5, BC = 2, а её площадь равна 28. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
126. B 8 № 340367. 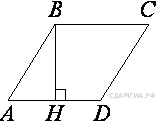 Высота BH ромба ABCD делит его сторону ADна отрезки AH = 5 и HD = 8. Найдите площадь ромба.
Высота BH ромба ABCD делит его сторону ADна отрезки AH = 5 и HD = 8. Найдите площадь ромба.
127. B 8 № 340408. 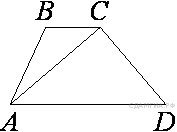 В трапеции ABCD AD = 3, BC = 1, а её площадь равна 12. Найдите площадь треугольника ABC.
В трапеции ABCD AD = 3, BC = 1, а её площадь равна 12. Найдите площадь треугольника ABC.
Решения
1. B 8 № 39.  Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции равна произведению полусуммы оснований на высоту:
![]()
Ответ: 168.
2. B 8 № 65.  Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
Решение.
Площадь параллелограмма равна произведению длины основания на высоту:
![]()
Ответ: 40.
3. B 8 № 91. Найдите площадь параллелограмма, изображённого на рисунке.
Решение.
Площадь параллелограмма равна произведению длины основания на высоту:
![]()
Ответ: 75.
4. B 8 № 117.  Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции равна произведению полусуммы оснований на высоту:
![]()
Ответ: 28.
5. B 8 № 143.  Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции равна произведению полусуммы оснований на высоту:
![]()
Ответ: 36.
6. B 8 № 195.  Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
Решение.
Площадь параллелограмма равна произведению длины основания на высоту:
![]()
Ответ: 20.
7. B 8 № 169839. В прямоугольном треугольнике один из катетов равен 10, а острый угол, прилежащий к нему, равен ![]() . Найдите площадь треугольника.
. Найдите площадь треугольника.
Решение.
Пусть x — длина второго катета. Так как треугольник прямоугольный, по определению тангенса имеем:
![]()
.
Площадь прямоугольного треугольника равна половине произведения катетов. Таким образом:
![]()
.
———-
Иррациональный ответ.
8. B 8 № 169840. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.
Решение.
Так как в прямоугольном треугольнике один из углов равен 45°, то такой треугольник является равнобедренным. Площадь прямоугольного треугольника равна половине произведения катетов. Таким образом:
![]()
Ответ: 50.
9. B 8 № 169841. В прямоугольном треугольнике один из катетов равен 10, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
Решение.
Так как в прямоугольном треугольнике один из углов равен 45°, треугольник является равнобедренным. Площадь прямоугольного треугольника равна половине произведения катетов. Таким образом:
![]()
Ответ: 50.
10. B 8 № 169842. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен ![]() . Найдите площадь треугольника.
. Найдите площадь треугольника.
Решение.
Пусть x — длина второго катета. Так как треугольник прямоугольный, по определению тангенса имеем:
![]()
.
Площадь прямоугольного треугольника равна половине произведения катетов. Таким образом:
![]()
.
———-
Иррациональный ответ.
11. B 8 № 169847. Сторона равностороннего треугольника равна 10. Найдите его площадь,делённую на ![]() .
.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Так как угол равностороннего треугольника равен 60° и все стороны равны 10, имеем:
![]()
Ответ: 25.
———-
В открытом банке иррациональный ответ.
12. B 8 № 169848. Периметр равностороннего треугольника равен 30. Найдите его площадь,делённую на ![]() .
.
Решение.
Так как в равностороннем треугольнике все стороны равны, то сторона данного треугольника равна 10. Угол равностороннего треугольника равен 60°. Площадь треугольника равна половине произведения сторон на синус угла между ними, имеем:
![]()
Ответ: 25.
———-
В открытом банке иррациональный ответ.
13. B 8 № 169849. Высота равностороннего треугольника равна 10. Найдите его площадь,делённую на ![]()
Решение.
Высота равностороннего треугольника равна ![]() Таким образом, сторона равностороннего треугольника равна
Таким образом, сторона равностороннего треугольника равна ![]() Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
![]()
Ответ: 100.
———-
В открытом банке иррациональный ответ.
14. B 8 № 169850. В равнобедренном треугольнике боковая сторона равна 10, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, делённую на ![]()
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними, имеем:
![]()
Ответ: 25.
———-
В открытом банке иррациональный ответ.
15. B 8 № 169851. Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.
Решение.
Так как боковая сторона равнобедренного треугольника равна 5, его основание равно 6, а полупериметр: ![]() тогда по формуле Герона имеем:
тогда по формуле Герона имеем:
![]()
Ответ: 12.
16. B 8 № 169852. Периметр равнобедренного треугольника равен 16, а основание — 6. Найдите площадь треугольника.
Решение.
Так как сторона основания равнобедренного треугольника равна 6, его боковая сторона 5, а полупериметр: ![]() тогда по формуле Герона имеем:
тогда по формуле Герона имеем:
![]()
Ответ: 12.
17. B 8 № 169853. В треугольнике одна из сторон равна 10, а опущенная на нее высота — 5. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения высоты на основание. Таким образом:
![]()
Ответ: 25.
18. B 8 № 169854. В треугольнике одна из сторон равна 10, другая равна ![]() , а угол между ними равен 60°. Найдите площадь треугольника.
, а угол между ними равен 60°. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
![]()
Ответ: 75.
19. B 8 № 169855. В треугольнике одна из сторон равна 10, другая равна ![]() , а угол между ними равен 45°. Найдите площадь треугольника.
, а угол между ними равен 45°. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
![]()
Ответ: 50.
20. B 8 № 169856. В треугольнике одна из сторон равна 10, другая равна ![]() , а угол между ними равен 120°. Найдите площадь треугольника.
, а угол между ними равен 120°. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
![]()
Ответ: 75.
21. B 8 № 169857. В треугольнике одна из сторон равна 10, другая равна ![]() , а угол между ними равен 135°. Найдите площадь треугольника.
, а угол между ними равен 135°. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
![]()
Ответ: 50.
22. B 8 № 169858. В треугольнике одна из сторон равна 10, другая равна 12, а угол между ними равен 30°. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
![]()
Ответ: 30.
23. B 8 № 169859. В треугольнике одна из сторон равна 12, другая равна 16, а синус угла между ними равен ![]() . Найдите площадь треугольника.
. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
![]()
Ответ: 24.
24. B 8 № 169860. В треугольнике одна из сторон равна 12, другая равна 10, а косинус угла между ними равен ![]() . Найдите площадь треугольника.
. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Cинус угла найдем из основного тригонометрического тождества:
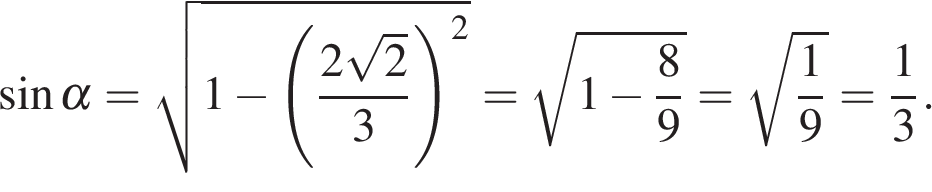
Таким образом,
![]()
Ответ: 20.
25. B 8 № 169862. Сторона квадрата равна 10. Найдите его площадь.
Решение.
Площадь квадрата равна квадрату его стороны, поэтому она равна 100.
Ответ: 100.
26. B 8 № 169863. Периметр квадрата равен 40. Найдите площадь квадрата.
Решение.
Периметр квадрата равен сумме длин всех его сторон. Таким образом, сторона квадрата равна 10. Площадь квадрата равна квадрату его стороны, поэтому она равна 100.
Ответ: 100.
27. B 8 № 169864. В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
Решение.
Площадь прямоугольника равна произведению его смежных сторон, поэтому она равна 120.
Ответ: 120.
28. B 8 № 169865. В прямоугольнике одна сторона равна 10, периметр равен 44. Найдите площадь прямоугольника.
Решение.
Противоположные стороны прямоугольника попарно равны. Пусть неизвестная сторона равна x, тогда периметр прямоугольника: 2x + 20 = 44, откуда x = 12. Площадь прямоугольника равна произведению его смежных сторон, поэтому она равна 120.
Ответ: 120.
29. B 8 № 169866. В прямоугольнике одна сторона равна 6, а диагональ равна 10. Найдите площадь прямоугольника.
Решение.
Диагональ прямоугольника делит его на два прямоугольных треугольника. По теореме Пифагора найдем длину неизвестной стороны, она равна ![]() Площадь прямоугольника равна произведению его смежных сторон. Таким образом,
Площадь прямоугольника равна произведению его смежных сторон. Таким образом,
![]()
Ответ: 48.
30. B 8 № 169867. В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 30°. Найдите площадь прямоугольника, делённую на ![]() .
.
Решение.
Диагональ прямоугольника делит его на два прямоугольных треугольника. Катет прямоугольного треугольника, лежащий напротив угла в 30°, равен половине гипотенузы. Поэтому одна из сторон прямоугольника равна 5. По теореме Пифагора найдем вторую строну: ![]() Площадь прямоугольника равна произведению его смежных сторон, имеем:
Площадь прямоугольника равна произведению его смежных сторон, имеем:
![]()
Ответ: 25.
———-
В открытом банке иррациональный ответ.
31. B 8 № 169868. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
Решение.
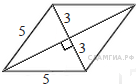 Диагонали ромба пересекаются под углом 90° и точкой пересечения делятся пополам. Из прямоугольного треугольника, катетами которого являются половины диагоналей ромба, а гипотенузой — сторона ромба, по теореме Пифагора найдем половину неизвестной диагонали:
Диагонали ромба пересекаются под углом 90° и точкой пересечения делятся пополам. Из прямоугольного треугольника, катетами которого являются половины диагоналей ромба, а гипотенузой — сторона ромба, по теореме Пифагора найдем половину неизвестной диагонали: ![]() Тогда вся неизвестная диагональ равна 8.
Тогда вся неизвестная диагональ равна 8.
Площадь ромба равна половине произведения диагоналей:
![]()
Ответ: 24.
32. B 8 № 169869. Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.
Решение.
Периметр ромба равен сумме длин всех его сторон. Так как все стороны равны, сторона ромба равна 10. Площадь ромба равна произведению сторон на синус угла между ними. Таким образом,
![]()
Ответ: 50.
33. B 8 № 169870. Периметр ромба равен 40, а один из углов равен 45°. Найдите площадь ромба,делённую на ![]() .
.
Решение.
Так как все стороны ромба равны, сторона данного ромба равна 10. Площадь ромба равна произведению сторон на синус угла между ними, поэтому
![]()
Ответ: 50.
———-
В открытом банке иррациональный ответ.
34. B 8 № 169871. Периметр ромба равен 40, а один из углов равен 60°. Найдите площадь ромба,делённую на ![]() .
.
Решение.
Так как все стороны ромба равны, сторона данного ромба равна 10. Площадь ромба равна произведению сторон на синус угла между ними, поэтому
![]()
Ответ: 50.
———-
В открытом банке иррациональный ответ.
35. B 8 № 169872. Периметр ромба равен 24, а синус одного из углов равен ![]() . Найдите площадь ромба.
. Найдите площадь ромба.
Решение.
Периметр ромба равен сумме длин всех его сторон. Так как все стороны равны, сторона ромба равна 6. Площадь ромба равна произведению сторон на синус угла между ними, поэтому
![]()
Ответ: 12.
36. B 8 № 169873. Периметр ромба равен 24, а косинус одного из углов равен ![]() . Найдите площадь ромба.
. Найдите площадь ромба.
Решение.
Периметр ромба равен сумме длин всех его сторон. Так как все стороны равны, сторона ромба равна 6. Площадь ромба равна произведению сторон на синус угла между ними. Синус угла найдем из основного тригонометрического тождества:
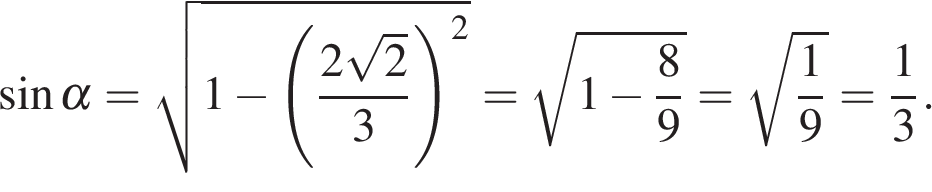
Таким образом,
![]()
Ответ: 12.
37. B 8 № 169874. Периметр ромба равен 24, а тангенс одного из углов равен ![]() . Найдите площадь ромба.
. Найдите площадь ромба.
Решение.
Периметр ромба равен сумме длин всех его сторон. Так как все стороны равны, сторона ромба равна 6. Площадь ромба равна произведению сторон на синус угла между ними. Найдем синус угла. В прямоугольном треугольнике тангенс определяется как отношение противолежащего катета к прилежащему. Имеем:
![]()
Таким образом, ![]() , где x — число.
, где x — число.
По теореме Пифагора гипотенуза этого прямоугольного треугольника равна:
![]()
.
В прямоугольном треугольнике синус определяется как отношение противолежащего катета к гипотенузе. Имеем:
![]()
Таким образом,
![]()
Ответ: 12.
38. B 8 № 169875. Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.
Решение.
Площадь параллелограмма равна произведению высоты на основание. Таким образом,
![]()
Ответ: 120.
39. B 8 № 169876. Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на ![]() .
.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними:
![]()
Ответ: 30.
———-
В открытом банке иррациональный ответ.
40. B 8 № 169877. Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 60°. Найдите площадь параллелограмма, делённую на ![]() .
.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними:
![]()
Ответ: 30.
———-
В открытом банке иррациональный ответ.
41. B 8 № 169878. Одна из сторон параллелограмма равна 12, другая равна 5, а синус одного из углов равен ![]() . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними, поэтому
![]()
Ответ: 20.
42. B 8 № 169879. Одна из сторон параллелограмма равна 12, другая равна 5, а косинус одного из углов равен ![]() . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними. Cинус угла найдем из основного тригонометрического тождества:
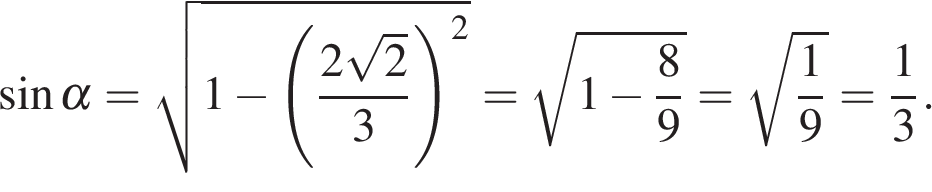
Таким образом,
![]()
Ответ: 20.
43. B 8 № 169880. Одна из сторон параллелограмма равна 12, другая равна 5, а тангенс одного из углов равен ![]() . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними. Найдем синус угла. В прямоугольном треугольнике тангенс определяется как отношение противолежащего катета к прилежащему. Имеем:
![]()
Таким образом, ![]() , где x — число.
, где x — число.
По теореме Пифагора гипотенуза этого прямоугольного треугольника равна:
![]()
.
В прямоугольном треугольнике синус определяется как отношение противолежащего катета к гипотенузе. Имеем:
![]()
Таким образом,
![]()
Ответ: 20.
44. B 8 № 169881. Основания трапеции равны 18 и 12, одна из боковых сторон равна ![]() , а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
, а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
Решение.
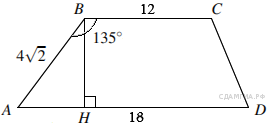 Пусть дана трапеция ABCD, где AD = 18, BC = 12, AB =
Пусть дана трапеция ABCD, где AD = 18, BC = 12, AB = ![]() , а ∠ABC = 135°. Опустим перпендикуляр BH на сторону AD. Угол ABH равен: 135° − 90° = 45°. Таким образом треугольник ABH является прямоугольным и равнобедренным. Найдем высоту BH:
, а ∠ABC = 135°. Опустим перпендикуляр BH на сторону AD. Угол ABH равен: 135° − 90° = 45°. Таким образом треугольник ABH является прямоугольным и равнобедренным. Найдем высоту BH:
![]()
Площадь трапеции равна полусумме оснований на высоту:
![]()
Ответ: 60.
45. B 8 № 169882. Основания трапеции равны 18 и 10, одна из боковых сторон равна ![]() , а угол между ней и одним из оснований равен 120°. Найдите площадь трапеции.
, а угол между ней и одним из оснований равен 120°. Найдите площадь трапеции.
Решение.
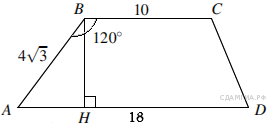 Пусть дана трапеция ABCD, где AD = 18, BC = 10, AB =
Пусть дана трапеция ABCD, где AD = 18, BC = 10, AB = ![]() , а ∠ABC = 120°. Опустим перпендикуляр BH на сторону AD. Угол ABH равен: 120° − 90° = 30°. Найдем высоту BH:
, а ∠ABC = 120°. Опустим перпендикуляр BH на сторону AD. Угол ABH равен: 120° − 90° = 30°. Найдем высоту BH:
![]()
Площадь трапеции равна полусумме оснований на высоту:
![]()
Ответ: 84.
46. B 8 № 169883. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а синус угла между ней и одним из оснований равен ![]() . Найдите площадь трапеции.
. Найдите площадь трапеции.
Решение.
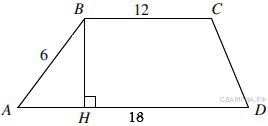 Пусть дана трапеция ABCD, где AD = 18, BC = 12, AB = 6, а
Пусть дана трапеция ABCD, где AD = 18, BC = 12, AB = 6, а ![]() Опустим перпендикуляр BH на сторонуAD. Найдем высоту BH:
Опустим перпендикуляр BH на сторонуAD. Найдем высоту BH:
![]()
Площадь трапеции равна полусумме оснований на высоту:
![]()
Ответ: 30.
47. B 8 № 169884. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а косинус угла между ней и одним из оснований равен ![]() . Найдите площадь трапеции.
. Найдите площадь трапеции.
Решение.
Пусть дана трапеция ABCD, где AD = 18, BC = 12, AB = 6, а ![]() Опустим перпендикулярBH на сторону AD. Найдем синус угла из основного тригонометрического тождества:
Опустим перпендикулярBH на сторону AD. Найдем синус угла из основного тригонометрического тождества:
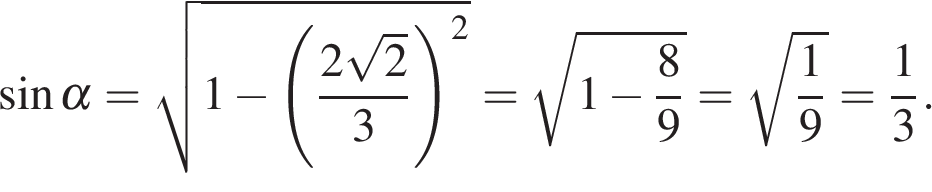
Найдем высоту BH:
![]()
Площадь трапеции равна полусумме оснований на высоту:
![]()
Ответ: 30.
48. B 8 № 169885. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а тангенс угла между ней и одним из оснований равен ![]() . Найдите площадь трапеции.
. Найдите площадь трапеции.
Решение.
Пусть дана трапеция ABCD, где AD = 18, BC = 12, AB = 6, а ![]() Опустим перпендикулярBH на сторону AD. Найдем синус угла. В прямоугольном треугольнике тангенс определяется как отношение противолежащего катета к прилежащему. Имеем:
Опустим перпендикулярBH на сторону AD. Найдем синус угла. В прямоугольном треугольнике тангенс определяется как отношение противолежащего катета к прилежащему. Имеем:
![]()
Таким образом, ![]() , где x — число.
, где x — число.
По теореме Пифагора гипотенуза этого прямоугольного треугольника равна:
![]()
.
В прямоугольном треугольнике синус определяется как отношение противолежащего катета к гипотенузе. Имеем:
![]()
Найдем высоту BH:
![]()
Площадь трапеции равна полусумме оснований на высоту:
![]()
Ответ: 30.
49. B 8 № 169886. Радиус круга равен 1. Найдите его площадь, деленную на π.
Решение.
Площадь круга равна:
![]()
Ответ: 1.
—————
В открытом банке ответ c числом π.
50. B 8 № 169887. Найдите площадь кругового сектора, если радиус круга равен 3, а угол сектора равен 120°. В ответе укажите площадь, деленную на π.
Решение.
Площадь сектора равна:
![]()
Ответ: 3.
—————
В открытом банке ответ с числом π.
51. B 8 № 169888. Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6π, а угол сектора равен 120°. В ответе укажите площадь, деленную на π.
Решение.
Найдем радиус сектора из формулы длины дуги:
![]()
.
Площадь сектора равна:
![]()
Ответ: 27.
—————
В открытом банке ответ с числом π.
52. B 8 № 169889. В прямоугольном треугольнике один из катетов равен 10, острый угол, прилежащий к нему, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на ![]() .
.
Решение.
 Найдем второй катет треугольника из определения тангенса:
Найдем второй катет треугольника из определения тангенса:
![]()
Площадь прямоугольного треугольника равна половине произведения катетов:
![]()
Ответ: 50.
Примечание:
Второй катет можно было найти при помощи теоремы Пифагора.
———-
В открытом банке иррациональный ответ.
53. B 8 № 169890. В прямоугольном треугольнике один из катетов равен ![]() , острый угол, прилежащий к нему, равен 30°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на
, острый угол, прилежащий к нему, равен 30°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на ![]() .
.
Решение.
 Катет, лежащий напротив угла в 30°, равен половине гипотенузы, поэтому AC = 10. Площадь прямоугольного треугольника равна половине произведения катетов:
Катет, лежащий напротив угла в 30°, равен половине гипотенузы, поэтому AC = 10. Площадь прямоугольного треугольника равна половине произведения катетов:
![]()
Ответ: 50.
———-
В открытом банке иррациональный ответ.
54. B 8 № 169891. В прямоугольном треугольнике один из катетов равен 10, угол, лежащий напротив него, равен 30°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на ![]() .
.
Решение.
 Найдем второй катет по теореме Пифагора:
Найдем второй катет по теореме Пифагора:
![]()
Площадь прямоугольного треугольника равна половине произведения катетов:
![]()
Ответ: 50.
Примечание:
Второй катет можно было найти из определения тангенса.
———-
В открытом банке иррациональный ответ.
55. B 8 № 169892. В прямоугольном треугольнике один из катетов равен ![]() , угол, лежащий напротив него, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на
, угол, лежащий напротив него, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на ![]() .
.
Решение.
 Найдем второй катет по теореме Пифагора:
Найдем второй катет по теореме Пифагора:
![]()
Площадь прямоугольного треугольника равна половине произведения катетов:
![]()
Ответ: 50.
Примечание:
Второй катет можно было найти из определения тангенса или из свойства угла, лежащего напротив 30°.
———-
В открытом банке иррациональный ответ.
56. B 8 № 169893. В равнобедренном треугольнике боковая сторона равна 10, основание — ![]() , а угол, лежащий напротив основания, равен 30°. Найдите площадь треугольника.
, а угол, лежащий напротив основания, равен 30°. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними:
![]()
Ответ: 25.
Примечание:
Площадь треугольника можно было найти по формуле Герона.
57. B 8 № 169894. В равнобедренном треугольнике боковая сторона равна 10, основание — ![]() , а угол, лежащий напротив основания, равен 45°. Найдите площадь треугольника, деленную на
, а угол, лежащий напротив основания, равен 45°. Найдите площадь треугольника, деленную на ![]()
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними:
![]()
Ответ: 25.
Примечание:
Площадь треугольника можно было найти по формуле Герона.
———-
В открытом банке иррациональный ответ.
58. B 8 № 169895. В равнобедренном треугольнике боковая сторона равна 10, основание — ![]() , а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, деленную на
, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, деленную на ![]()
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними:
![]()
Ответ: 25.
Примечание:
Площадь треугольника можно было найти по формуле Герона.
———-
В открытом банке иррациональный ответ.
59. B 8 № 169896. В равнобедренном треугольнике боковая сторона равна 10, основание — ![]() , а угол, лежащий напротив основания, равен 135°. Найдите площадь треугольника, деленную на
, а угол, лежащий напротив основания, равен 135°. Найдите площадь треугольника, деленную на ![]()
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними:
![]()
Ответ: 25.
Примечание:
Площадь треугольника можно было найти по формуле Герона.
———-
В открытом банке иррациональный ответ.
60. B 8 № 169897. В равнобедренном треугольнике боковая сторона равна 10, основание — ![]() , а угол, лежащий напротив основания, равен 150°. Найдите площадь треугольника.
, а угол, лежащий напротив основания, равен 150°. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними:
![]()
Ответ: 25.
Примечание:
Площадь треугольника можно было найти по формуле Герона.
61. B 8 № 169898. В прямоугольнике диагональ равна 10, угол между ней и одной из сторон равен 30°, длина этой стороны ![]() . Найдите площадь прямоугольника, деленную на
. Найдите площадь прямоугольника, деленную на ![]()
Решение.
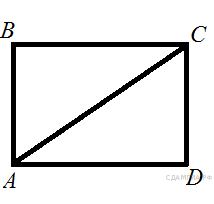 Диагональ прямоугольника делит его на два прямоугольных треугольника. Катет, лежащий напротив угла в 30°, равен половине гипотенузы, поэтомуСD = 5. Площадь прямоугольника равна произведению его сторон:
Диагональ прямоугольника делит его на два прямоугольных треугольника. Катет, лежащий напротив угла в 30°, равен половине гипотенузы, поэтомуСD = 5. Площадь прямоугольника равна произведению его сторон:
![]()
Ответ: 25.
Примечание:
Вторую сторону можно было найти из определения синуса.
———-
В открытом банке иррациональный ответ.
62. B 8 № 169899. В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 60°, длина этой стороны равна 5. Найдите площадь прямоугольника, деленную на ![]()
Решение.
 Найдем вторую сторону по теореме Пифагора:
Найдем вторую сторону по теореме Пифагора:
![]()
Площадь прямоугольника равна произведению его сторон:
![]()
Ответ: 25.
Примечание:
Вторую сторону можно было найти из определения синуса.
———-
В открытом банке иррациональный ответ.
63. B 8 № 169900. В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, лежащий напротив этой диагонали, равен 30°. Найдите площадь ромба.
, а угол, лежащий напротив этой диагонали, равен 30°. Найдите площадь ромба.
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
![]()
Ответ:50.
Примечание:
Можно найти вторую диагональ по теореме косинусов и вычислить площадь ромба как половина произведения диагоналей.
64. B 8 № 169901. В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, лежащий напротив этой диагонали, равен 45°. Найдите площадь ромба, деленную на
, а угол, лежащий напротив этой диагонали, равен 45°. Найдите площадь ромба, деленную на ![]()
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
![]()
Ответ:50.
———-
В открытом банке иррациональный ответ.
65. B 8 № 169902. В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, лежащий напротив этой диагонали, равен 120°. Найдите площадь ромба, деленную на
, а угол, лежащий напротив этой диагонали, равен 120°. Найдите площадь ромба, деленную на ![]()
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
![]()
Ответ: 50.
Примечание:
Можно найти вторую диагональ по теореме косинусов и вычислить площадь ромба как половина произведения диагоналей.
———-
В открытом банке иррациональный ответ.
66. B 8 № 169903. В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, лежащий напротив этой диагонали, равен 135°. Найдите площадь ромба, деленную на
, а угол, лежащий напротив этой диагонали, равен 135°. Найдите площадь ромба, деленную на ![]()
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
![]()
Ответ:50.
———-
В открытом банке иррациональный ответ.
67. B 8 № 169904. В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, лежащий напротив этой диагонали, равен 150°. Найдите площадь ромба.
, а угол, лежащий напротив этой диагонали, равен 150°. Найдите площадь ромба.
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
![]()
Ответ:50.
Примечание:
Можно найти вторую диагональ по теореме косинусов и вычислить площадь ромба как половина произведения диагоналей.
68. B 8 № 169905. В ромбе сторона равна 10, одна из диагоналей — 10, а угол, лежащий напротив этой диагонали, равен 60°. Найдите площадь ромба, деленную на ![]()
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
![]()
Ответ: 50.
69. B 8 № 169906. В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, из которого выходит эта диагональ, равен 150°. Найдите площадь ромба.
, а угол, из которого выходит эта диагональ, равен 150°. Найдите площадь ромба.
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
![]()
Ответ:50.
Примечание:
Можно найти вторую диагональ по теореме косинусов и вычислить площадь ромба как половина произведения диагоналей.
70. B 8 № 169908. В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, из которого выходит эта диагональ, равен 60°. Найдите площадь ромба, деленную на
, а угол, из которого выходит эта диагональ, равен 60°. Найдите площадь ромба, деленную на ![]()
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
![]()
Ответ: 50.
71. B 8 № 169909. В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, из которого выходит эта диагональ, равен 45°. Найдите площадь ромба, деленную на
, а угол, из которого выходит эта диагональ, равен 45°. Найдите площадь ромба, деленную на ![]()
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
![]()
Ответ:50.
———-
В открытом банке иррациональный ответ.
72. B 8 № 169910. В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, из которого выходит эта диагональ, равен 30°. Найдите площадь ромба.
, а угол, из которого выходит эта диагональ, равен 30°. Найдите площадь ромба.
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
![]()
Ответ:50.
Примечание:
Можно найти вторую диагональ по теореме косинусов и вычислить площадь ромба как половина произведения диагоналей.
73. B 8 № 169911. В ромбе сторона равна 10, одна из диагоналей — 10, а угол, из которого выходит эта диагональ, равен 120°. Найдите площадь ромба, деленную на ![]()
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
![]()
Ответ:50.
Примечание:
Можно найти вторую диагональ по теореме косинусов и вычислить площадь ромба как половина произведения диагоналей.
74. B 8 № 169912. Радиус круга равен 3, а длина ограничивающей его окружности равна 6π. Найдите площадь круга. В ответ запишите площадь, деленную на π.
Решение.
Площадь круга равна ![]() имеем:
имеем:
![]()
Ответ: 9.
———-
В открытом банке ответ с числом ![]() .
.
75. B 8 № 169913. Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6π, угол сектора равен 120°, а радиус круга равен 9. В ответ укажите число, деленную на π.
Решение.
Площадь сектора равна ![]() имеем:
имеем:
![]()
Ответ: 27.
76. B 8 № 311332. В равнобедренном треугольнике ![]() . Найдите
. Найдите ![]() , если высота
, если высота ![]() .
.
Решение.
В равнобедренном треугольнике высота, опущенная на основание делит основание пополам, то есть ![]() делит
делит ![]() пополам. Тогда получаем прямоугольный треугольник
пополам. Тогда получаем прямоугольный треугольник ![]() с двумя известными катетами
с двумя известными катетами ![]() и
и ![]() гипотенузой которого является искомая
гипотенузой которого является искомая ![]() По теореме Пифагора найдем
По теореме Пифагора найдем
![]()
Ответ: 13.
77. B 8 № 311375. В равнобедренном треугольнике ![]() . Найдите
. Найдите ![]() , если высота
, если высота ![]() .
.
Решение.
По теореме Пифагора имеем:
![]()
Так как высота в равнобедренном треугольнике является медианой, то
![]()
Ответ: 12.
78. B 8 № 311387. В треугольнике ![]() угол
угол ![]() равен 90°,
равен 90°, ![]() . Найдите
. Найдите ![]() .
.
Решение.
Так как треугольник ABC — прямоугольный, то ![]() . Имеем:
. Имеем:
![]()
Ответ: 21.
79. B 8 № 311399. В треугольнике ![]() угол
угол ![]() равен 90°,
равен 90°, ![]() . Найдите
. Найдите ![]() .
.
Решение.
Так как треугольник ABC — прямоугольный, то ![]() . Имеем:
. Имеем:
![]()
Ответ: 33.
80. B 8 № 311411. Основания трапеции равны 4 см и 10 см. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.

Решение.
Пусть KN — средняя линия трапеции, где L — точка пересечения с диагональю.
![]()
Так как KN — средняя линия трапеции, то KL и LN средние линии треугольников ABC и СAD соответственно.
![]() ,
, ![]()
Ответ: 5.
81. B 8 № 311475. Диагональ трапеции делит её среднюю линию на отрезки, равные 4 см и 3 см. Найдите меньшее основание трапеции.
Решение.
Пусть KN — средняя линия трапеции, где L — точка пересечения с диагональю.
Так как KN — средняя линия трапеции , то KL и LN средние линии треугольников ABC и СAD соответственно.
![]()
![]()
Таким образом, длина меньшего основания равна 6 см.
Ответ: 6.
82. B 8 № 311480. Средняя линия трапеции равна 11, а меньше основание равно 5. Найдите большее основание трапеции.

Решение.
Средняя линия трапеции равна полусумме оснований. Имеем:
![]()
Ответ: 17.
83. B 8 № 311498. В треугольнике ![]() угол
угол ![]() прямой,
прямой, ![]() . Найдите
. Найдите ![]() .
.
Решение.
Треугольник ABC — прямоугольный. Таким образом,
![]()
![]()
Ответ: 20.
84. B 8 № 311500.  В треугольнике
В треугольнике ![]() угол
угол ![]() прямой,
прямой, ![]() . Найдите
. Найдите ![]() .
.
Решение.
Треугольник ABC — прямоугольный. Таким образом,
![]()
![]()
Ответ: 30.
85. B 8 № 311682.  Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Решение.
По формуле площади трапеции имеем:
![]()
Ответ: 168.
86. B 8 № 311761. Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой.
Решение.
Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника. Пусть x — меньшая сторона прямоугольника. Тогда периметр прямоугольника равен ![]() откуда
откуда ![]() Поэтому площадь прямоугольника равна
Поэтому площадь прямоугольника равна ![]()
Ответ: 120.
87. B 8 № 311849. Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.
Решение.
Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника. Пусть x — большая сторона прямоугольника, тогда другая сторона равна ![]() Следовательно, периметр прямоугольника равен
Следовательно, периметр прямоугольника равен
![]()
откуда ![]() Поэтому площадь прямоугольника равна
Поэтому площадь прямоугольника равна ![]()
Ответ: 176.
88. B 8 № 311913.  Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
Решение.
Площадь параллелограмма равна произведению основания на высоту: 7 · 4 = 28.
Ответ: 28.
89. B 8 № 311957.
Найдите площадь параллелограмма, изображённого на рисунке.
Решение.
Площадь параллелограмма равна произведению основания на высоту: 24 · (2 + 7) = 216.
Ответ: 216.
90. B 8 № 314870.  Площадь параллелограмма ABCD равна 56. Точка E — середина стороны CD. Найдите площадь трапецииAECB.
Площадь параллелограмма ABCD равна 56. Точка E — середина стороны CD. Найдите площадь трапецииAECB.
Решение.
Диагональ параллелограмма делит его на два равных треугольника, поэтому ![]() Медиана треугольника делит его на два равновеликих треугольника, поэтому
Медиана треугольника делит его на два равновеликих треугольника, поэтому ![]() Следовательно,
Следовательно,
![]()
Ответ: 42.
91. B 8 № 314876.  Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Решение.
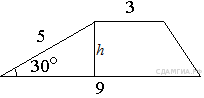 Площадь трапеции вычисляется по формуле
Площадь трапеции вычисляется по формуле
![]() где
где ![]() и
и ![]() — основания, а
— основания, а ![]() — высота трапеции. Найдём высоту:
— высота трапеции. Найдём высоту: ![]() следовательно,
следовательно, ![]()
Ответ: 15.
92. B 8 № 314882.  В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Решение.
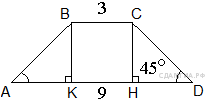 Введём обозначения, как показано на рисунке. Тогда
Введём обозначения, как показано на рисунке. Тогда ![]() Треугольник
Треугольник ![]() прямоугольный и равнобедренный, тогда высота
прямоугольный и равнобедренный, тогда высота ![]() равна 3. Откуда
равна 3. Откуда ![]()
Ответ: ![]()
93. B 8 № 315000.  Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
Решение.
Площадь параллелограмма равна произведению высоты на основание, поэтому она равна ![]()
Ответ: 20.
94. B 8 № 315074.  Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
Решение.

Найдите площадь параллелограмма, изображённого на рисунке.
95. B 8 № 315084.  Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
Решение.

Найдите площадь параллелограмма, изображённого на рисунке.
96. B 8 № 316231. Найдите площадь прямоугольника, если его периметр равен 92, а отношение соседних сторон равно 3:20.
Решение.
Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника. Пусть x — большая сторона прямоугольника, тогда другая сторона равна ![]() Следовательно, периметр прямоугольника равен
Следовательно, периметр прямоугольника равен
![]()
откуда ![]() Поэтому площадь прямоугольника равна
Поэтому площадь прямоугольника равна ![]()
Ответ: 240.
——————
Дублирует задание 311817.
97. B 8 № 316258. Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.
Решение.
Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника. Пусть x — большая сторона прямоугольника, тогда другая сторона равна ![]() Следовательно, периметр прямоугольника равен
Следовательно, периметр прямоугольника равен
![]()
откуда ![]() Поэтому площадь прямоугольника равна
Поэтому площадь прямоугольника равна ![]()
Ответ: 176.
————————-
Дублирует задание 311849.
98. B 8 № 316284. Найдите площадь прямоугольника, если его периметр равен 102, а отношение соседних сторон равно 2:15.
Решение.
Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника. Пусть x — большая сторона прямоугольника, тогда другая сторона равна ![]() Следовательно, периметр прямоугольника равен
Следовательно, периметр прямоугольника равен
![]()
откуда ![]() Поэтому площадь прямоугольника равна
Поэтому площадь прямоугольника равна ![]()
Ответ: 270.
99. B 8 № 316321. Найдите площадь прямоугольника, если его периметр равен 58 и одна сторона на 5 больше другой.
Решение.
Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника. Пусть x — меньшая сторона прямоугольника, тогда другая сторона равна ![]() Следовательно, периметр прямоугольника равен
Следовательно, периметр прямоугольника равен
![]()
откуда ![]() Поэтому площадь прямоугольника равна
Поэтому площадь прямоугольника равна ![]()
Ответ: 204.
100. B 8 № 316347.  Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции вычисляется по формуле ![]() где
где ![]() и
и ![]() — основания, а
— основания, а ![]() — высота трапеции.
— высота трапеции.
![]()
Ответ: 324.
101. B 8 № 316373.  Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции вычисляется по формуле ![]() где
где ![]() и
и ![]() — основания, а
— основания, а ![]() — высота трапеции.
— высота трапеции.
![]()
Ответ: 270.
102. B 8 № 322861.  Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Решение.
Площадь получившейся фигуры равна разности площадей квадрата и прямоугольника: 6 · 6 − 4 · 2 = 28.
Ответ: 28.
103. B 8 № 323159. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
Решение.
Пусть катеты имеют длины ![]() и
и ![]() а гипотенуза — длину
а гипотенуза — длину ![]() Пусть длина высоты, проведённой к гипотенузе равна
Пусть длина высоты, проведённой к гипотенузе равна ![]() Найдём длину неизвестного катета из теоремы Пифагора:
Найдём длину неизвестного катета из теоремы Пифагора:
![]()
Площадь прямоугольного треугольника может быть найдена как половина произведения катетов:
![]()
Ответ: 672.
104. B 8 № 323179. ![]() Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
Решение.
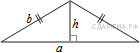 Пусть
Пусть ![]() — длина основания равнобедренного треугольника,
— длина основания равнобедренного треугольника, ![]() — длина боковой стороны равнобедренного треугольника,
— длина боковой стороны равнобедренного треугольника, ![]() — длина основания проведённого к высоте. Высота равнобедренного треугольника, проедённая к основанию, также является его биссектрисой и медианой. Из прямоугольного треугольника найдём высоту по теореме Пифагора:
— длина основания проведённого к высоте. Высота равнобедренного треугольника, проедённая к основанию, также является его биссектрисой и медианой. Из прямоугольного треугольника найдём высоту по теореме Пифагора:
![]()
Площадь треугольника равна половине произведения основания на высоту:
![]()
Ответ: 136.
105. B 8 № 323282. В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
Решение.
Сумма углов в треугольнике равна 180°, поэтому второй острый угол равен 180° − 90° − 45° = 45°. Оба острых угла равны, следовательно, данный треугольник — равнобедренный, откуда получаем, что второй катет равен 4. Площадь прямоугольного треугольника можно найти как половину произведения катетов: ![]()
Ответ: 8.
106. B 8 № 323285. В прямоугольном треугольнике один из катетов равен 35, а угол, лежащий напротив него равен 45∘. Найдите площадь треугольника.
Решение.
Сумма углов в треугольнике равна 180°, поэтому второй острый угол равен 180° − 90° − 45° = 45°. Оба острых угла равны, следовательно, данный треугольник — равнобедренный, откуда получаем, что второй катет равен 35. Площадь прямоугольного треугольника можно найти как половину произведения катетов: ![]()
Ответ: 612,5.
107. B 8 № 323297.
В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него равен 45∘. Найдите площадь треугольника.
108. B 8 № 323356.  В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
Решение.
Сумма углов в треугольнике равна 180°, поэтому второй острый угол равен 180° − 90° − 45° = 45°. Оба острых угла равны, следовательно, данный треугольник — равнобедренный, откуда получаем, что оба катета равны. Длина катета равна ![]() Площадь прямоугольного треугольника можно найти как половину произведения катетов:
Площадь прямоугольного треугольника можно найти как половину произведения катетов: ![]()
Ответ: 1225.
109. B 8 № 323396.  Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
Решение.
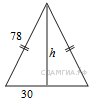 Периметр треугольника равен сумме длин его сторон, поэтому длина основания равна 216 − 78 − 78 = 60. Высота
Периметр треугольника равен сумме длин его сторон, поэтому длина основания равна 216 − 78 − 78 = 60. Высота ![]() проведённая к основанию равнобедренного треугольника, также является его биссектрисой и медианой, поэтому (см. рис.) имеем:
проведённая к основанию равнобедренного треугольника, также является его биссектрисой и медианой, поэтому (см. рис.) имеем:
![]()
Площадь треугольника равна половине произведения основания на высоту:
![]()
Ответ: 2160.
Примечание.
Пусть ![]() — полупериметр треугольника,
— полупериметр треугольника, ![]() — стороны треугольника. Можно не находить высоту, а найти площадь по формуле Герона:
— стороны треугольника. Можно не находить высоту, а найти площадь по формуле Герона:
![]()
![]()
110. B 8 № 323416. Периметр равнобедренного треугольника равен 196, а основание — 96. Найдите площадь треугольника.
Решение.
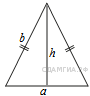 Пусть
Пусть ![]() — длина основания равнобедренного треугольника,
— длина основания равнобедренного треугольника, ![]() — длина боковой стороны равнобедренного треугольника,
— длина боковой стороны равнобедренного треугольника, ![]() — длина основания проведённого к высоте. Найдём длину боковой стороны:
— длина основания проведённого к высоте. Найдём длину боковой стороны:
![]()
Высота равнобедренного треугольника, проведённая к основанию, также является его биссектрисой и медианой. Из прямоугольного треугольника найдём высоту по теореме Пифагора:
![]()
Площадь треугольника равна половине произведения основания на высоту:
![]()
Ответ: 672.
Примечание.
Пусть ![]() — полупериметр треугольника. Можно не находить высоту, а найти площадь по формуле Герона:
— полупериметр треугольника. Можно не находить высоту, а найти площадь по формуле Герона:
![]()
![]()
111. B 8 № 323430.
Периметр равнобедренного треугольника равен 392, а основание – 192. Найдите площадь треугольника.
112. B 8 № 323436.  Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
Решение.
Площадь треугольника можно найти как половину произведения основания на высоту:
![]()
Ответ: 504.
113. B 8 № 323902.  Основания равнобедренной трапеции равны 5 и 17, а ее боковые стороны равны 10. Найдите площадь трапеции.
Основания равнобедренной трапеции равны 5 и 17, а ее боковые стороны равны 10. Найдите площадь трапеции.
Решение.
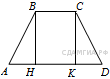 Проведём высоты в трапеции и введём обозначения как показано на рисунке. В четырёхугольнике
Проведём высоты в трапеции и введём обозначения как показано на рисунке. В четырёхугольнике ![]()
![]() И
И ![]() следовательно, он параллелограмм. Угол
следовательно, он параллелограмм. Угол ![]() значит,
значит, ![]() — прямоугольник, откуда
— прямоугольник, откуда ![]() и
и ![]() Поскольку трапеция равнобедренная, углы
Поскольку трапеция равнобедренная, углы ![]() и
и ![]() равны. Треугольники
равны. Треугольники ![]() и
и ![]() прямоугольные,
прямоугольные, ![]()
![]() следовательно, эти треугольники равны, откуда
следовательно, эти треугольники равны, откуда ![]() Из треугольника
Из треугольника ![]() по теореме Пифагора найдём высоту
по теореме Пифагора найдём высоту ![]()
![]()
Найдём площадь трапеции:
![]()
Ответ: 88.
114. B 8 № 323957.  Найдите площадь ромба, если его диагонали равны 14 и 6.
Найдите площадь ромба, если его диагонали равны 14 и 6.
Решение.
Площадь ромба можно найти как половину произведения его диагоналей: ![]()
Ответ: 42.
115. B 8 № 323977.  Периметр квадрата равен 160. Найдите площадь квадрата.
Периметр квадрата равен 160. Найдите площадь квадрата.
Решение.
Все стороны квадрата равны, поэтому сторона длина стороны квадрата равна ![]() Найдём площадь квадрата как квадрат его стороны:
Найдём площадь квадрата как квадрат его стороны: ![]()
Ответ: 1600.
116. B 8 № 323997.  Найдите площадь квадрата, если его диагональ равна 1.
Найдите площадь квадрата, если его диагональ равна 1.
Решение.
Диагонали квадрата равны. Площадь квадрата можно найти как половину произведения его диагоналей: ![]()
Ответ: 0,5.
117. B 8 № 324017.  Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
Решение.
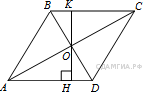 Проведём построение и введём обозначения как показано на рисунке. Учитывая, что
Проведём построение и введём обозначения как показано на рисунке. Учитывая, что ![]() и
и ![]() получаем
получаем ![]() Диагонали ромба точкой пересечения делятся пополам. Рассмотрим треугольники
Диагонали ромба точкой пересечения делятся пополам. Рассмотрим треугольники ![]() и
и ![]() , они прямоугольные,
, они прямоугольные, ![]()
![]() следовательно, треугольники
следовательно, треугольники ![]() и
и ![]() равны, откуда
равны, откуда ![]() то есть высота
то есть высота ![]() Найдём площадь ромба как произведение стороны на высоту:
Найдём площадь ромба как произведение стороны на высоту:
![]()
Ответ: 18.
118. B 8 № 324077.  В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
Решение.
Пусть a и b — длины сторон прямоугольника, c — длина диагонали. Рассмотрим прямоугольный треугольник, образованный диагональю и сторонами треугольника, из теоремы Пифагора найдём вторую сторону прямогуольника:
![]()
Найдём площадь прямоугольника как произведение его сторон:
![]()
Ответ: 2688.
119. B 8 № 324097.  Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.
Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.
Решение.
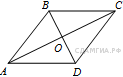 Введём обозначения как показано на рисунке. Диагонали ромба перпендикулярны и делятся точкой пересечения пополам. Пусть
Введём обозначения как показано на рисунке. Диагонали ромба перпендикулярны и делятся точкой пересечения пополам. Пусть ![]() Рассмотрим треугольник
Рассмотрим треугольник ![]() он прямоугольный, из теоремы Пифагора найдём
он прямоугольный, из теоремы Пифагора найдём ![]()
![]()
Найдём площадь ромба как половину произведения его диагоналей:
![]()
Ответ: 2400.
120. B 8 № 324117.  Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба.
Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба.
Решение.
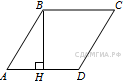 Проведём высоту в ромбе и введём обозначения как показано на рисунке. Все стороны ромба равны, поэтому
Проведём высоту в ромбе и введём обозначения как показано на рисунке. Все стороны ромба равны, поэтому ![]() Найдём
Найдём ![]() из прямоугольного треугольника
из прямоугольного треугольника ![]()
![]()
Найдём площадь ромба как произведение стороны на высоту:
![]()
Ответ: 420,5.
121. B 8 № 324155.  Основания трапеции равны 7 и 49, одна из боковых сторон равна 18 , а косинус угла между ней и одним из оснований равен
Основания трапеции равны 7 и 49, одна из боковых сторон равна 18 , а косинус угла между ней и одним из оснований равен ![]() Найдите площадь трапеции.
Найдите площадь трапеции.
Решение.
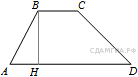 Проведём высоту и введём обозначения как показано на рисунке. Пусть сторона
Проведём высоту и введём обозначения как показано на рисунке. Пусть сторона ![]() тогда
тогда ![]() Из прямоугольного треугольника
Из прямоугольного треугольника ![]() найдём высоту
найдём высоту ![]()
![]()
Найдём площадь трапеции как произведение полусуммы оснований на высоту:
![]()
Ответ: 216.
122. B 8 № 324364.  Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Решение.
Пусть ![]() и
и ![]() соответственно радиус и диаметр окружности,
соответственно радиус и диаметр окружности, ![]() — сторона квадрата. Сторона квадрата равна диаметру вписанной окружности. Найдём площадь квадрата:
— сторона квадрата. Сторона квадрата равна диаметру вписанной окружности. Найдём площадь квадрата:
![]()
Ответ: 27 556.
123. B 8 № 339837.  Основания трапеции равны 1 и 13, одна из боковых сторон равна 152√, а угол между ней и одним из оснований равен 135∘. Найдите площадь трапеции.
Основания трапеции равны 1 и 13, одна из боковых сторон равна 152√, а угол между ней и одним из оснований равен 135∘. Найдите площадь трапеции.
Решение.
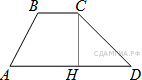 Проведём построения и введём обозначения как показано на рисунке. Отрезок
Проведём построения и введём обозначения как показано на рисунке. Отрезок ![]() — высота. Пусть угол
— высота. Пусть угол ![]() равен 135°. Сумма смежных углов трапеции, прилежащих к боковой стороне равна 180°, поэтому величина угла
равен 135°. Сумма смежных углов трапеции, прилежащих к боковой стороне равна 180°, поэтому величина угла ![]() равна 180° − 135° = 45°. Из прямоугольного треугольника
равна 180° − 135° = 45°. Из прямоугольного треугольника ![]() найдём высоту
найдём высоту ![]()
![]()
Площадь трапеции равна произведению полусуммы оснований на высоту:
![]()
Ответ: 105.
124. B 8 № 339859.  Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1 и HD = 28. Диагональ параллелограммаBD равна 53. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1 и HD = 28. Диагональ параллелограммаBD равна 53. Найдите площадь параллелограмма.
Решение.
Из прямоугольного треугольника ![]() по теореме Пифагора найдём
по теореме Пифагора найдём ![]()
![]()
Площадь параллелограмма равна произведению основания на высоту:
![]()
Ответ: 1305.
125. B 8 № 340197.  В трапеции ABCD AD = 5, BC = 2, а её площадь равна 28. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
В трапеции ABCD AD = 5, BC = 2, а её площадь равна 28. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
Решение.
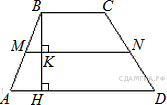 Проведём высоту
Проведём высоту ![]() Средняя линия равна полусумме оснований:
Средняя линия равна полусумме оснований: ![]() Площадь трапеции равна произведению полусуммы оснований на высоту:
Площадь трапеции равна произведению полусуммы оснований на высоту:
![]()
Поскольку ![]() — средняя линия,
— средняя линия, ![]() поэтому
поэтому ![]() Отрезки
Отрезки ![]() и
и ![]() равны,
равны, ![]() по теореме Фаллеса получаем, что
по теореме Фаллеса получаем, что ![]() Найдём площадь трапеции
Найдём площадь трапеции ![]()
![]()
Ответ: 11.
126. B 8 № 340367.  Высота BH ромба ABCD делит его сторону ADна отрезки AH = 5 и HD = 8. Найдите площадь ромба.
Высота BH ромба ABCD делит его сторону ADна отрезки AH = 5 и HD = 8. Найдите площадь ромба.
Решение.
Из прямоугольного треугольника ![]() найдём
найдём ![]()
![]()
Площадь ромба можно найти как произведение основания на высоту:
![]()
Ответ: 156.
127. B 8 № 340408.  В трапеции ABCD AD = 3, BC = 1, а её площадь равна 12. Найдите площадь треугольника ABC.
В трапеции ABCD AD = 3, BC = 1, а её площадь равна 12. Найдите площадь треугольника ABC.
Решение.
Пусть длина высоты трапеции равна ![]() Площадь трапеции можно найти как произведение полусуммы оснований на высоту:
Площадь трапеции можно найти как произведение полусуммы оснований на высоту:
![]()
Высота трапеции также является высотой треугольника ![]() Найдём площадь треугольника
Найдём площадь треугольника ![]() как полупроизведение основания на высоту:
как полупроизведение основания на высоту:
![]()
Ответ: 2.
Источники информации:
https://www.examen.ru/gia Экзамен.ру
https://sdamgia.ru Сдам ГИа
3. https://www.gia9.ru/ Тесты для ГИА. Содержатся все предметы, регистрация не нужна.
4.https://www.ctege.info — Подготовка к ЕГЭ и ГИА.
5. https://alexlarin.net ЕГЭ и ГИА
