Конспект урока для 11 класса «Применение элементов математического анализа при решении физических задач»

КОМБИНИРОВАННЫЙ УРОК

Аннотация

Урок построен на основе принципа действенного подхода к обучению, принципа сотрудничества, принципа обоснованного ответа.

Проблемно-диалогическая технология способствует обеспечению актуализации предметных знаний и умений учащихся, развития критического мышления, формирования коммуникативной культуры.

Применение информационной технологии способствует созданию наглядной опоры для обучения приемам анализа текста, созданию проблемно-диалогической ситуации, формированию исследовательских умений младших школьников.

Полноценное диалогическое общение на уроке возможно при соблюдении следующих условий:

— равенство личностных позиций учителя и ученика;

— приобретение нового знания в процессе рассуждения;

— предоставление возможности определить собственную позицию при наличии различных точек зрения;

— стимулирование самостоятельной поисковой деятельности учащихся.

Результатом урока являются глубоко осмысленные выводы учащихся, полное раскрытие замысла автора, высокий эмоциональный подъём и выход на нравственные ценности, составляющие духовность личности, её образовательную среду.

Урок представлялся на районный конкурс Урок года-2009 «Науки юношей питают…»

Тема: Применение элементов математического анализа при решении физических задач.

Цель: формировать умения учащихся применять методы матанализа при решении физических задач.

Задачи урока:

Предметные:

• выявить экспериментально зависимость силы тока в полной цепи от внешнего сопротивления;

• закрепить навыки вычисления производной для нахождения физических величин и нахождения наибольшего и наименьшего значений функции;

• закрепить знания закона Ома для полной цепи;

• способствовать формированию умений применять приёмы сравнения, обобщения, переноса знаний в новую ситуацию, развитию математического кругозора, мышления, речи;

• содействовать воспитанию интереса к математике и физике

Метапредметные:

познавательные:

• поиск и выделение необходимой информации;

• построение логической цепи рассуждений;

регулятивные:

• самостоятельное выделение и формулирование познавательной цели;

• целеполагание;

• контроль и оценка результатов деятельности;

• самооценка;

• развитие приёмов умственной деятельности, памяти, внимания, умения сопоставлять; анализировать, обобщать изучаемые факты;

коммуникативные:

• умение с достаточной полнотой и точностью выражать свои мысли;

• умение осознанно строить речевое высказывание в устной форме;

личностные:

• стимулирование учеников к самооценке образовательной деятельности;

• воспитание настойчивости в достижении цели и заинтересованности в конечном результате труда.

—Предполагаемые результаты:

Уметь: применять методы матанализа при решении физических задач;

вычислять производную для нахождения физических величин и нахождения наибольшего и наименьшего значений функции.

Знать: закон Ома для полной цепи, мощности; зависимость силы тока в полной цепи от внешнего сопротивления.

Тип урока: урок комплексного применения знаний умений и навыков.

Методы обучения:

• частично-поисковый,

• работа по опорным схемам,

• решение познавательных задач,

• системные обобщения.

Межпредметные связи: физика, математика, техника

Оборудование: источник тока, соединительные провода, амперметр, вольтметр, ключ.

Формы работы: фронтальная, индивидуальная, самостоятельная, парная.

Ход урока.

I. Организационный этап.

Учитель физики:

— Ребята! Сегодня у нас интегрированный урок математики и физики. Говорят, что математика – служанка всех наук, в том числе и физики. Зная математику, физики «вооружены». Им по силам не только простые задачи. Учёные давали математическое обоснование физическим законам и явлениям. Вы овладеваете таким математическим аппаратом, чтобы познавать мир и объяснять его.

Сегодня мы поговорим о применении производной и использовании математического анализа для решения физических задач.

?- Какие физические величины можно определить с помощью производной?

— скорость, ускорение, силу, импульс, кинетическую энергию, если известно ускорение движения, силу тока, напряжение, мощность, если известно уравнение изменения заряда.

II. Повторение опорных знаний.

Учитель математики:

— Давайте вспомним правила нахождения производных и некоторые физические формулы. Проверьте, пожалуйста, все ли формулы на доске записаны верно?

— На уроках физики вам довольно часто требуется установить зависимость одной физической величины от другой. Математические исследования могут помочь вам в этом.

Задание №1 Исследовать зависимость силы тока от внешнего сопротивления.

(два ученика выполняют экспериментальное задание)

Учитель физики:

— С помощью графиков можно определять физические величины.

— Как зависит сила тока от внешнего сопротивления? Запишите формулу.

Вид формулы закона Ома такой же как вид функции

Аргумент – R. R>0. Почему?

— Следовательно, интересующий нас график будет выглядеть следующим образом. (Убирается лишнее на графике, меняется обозначение осей координат.)

— Точка пересечения графика с осью ординат есть значение тока при R=0.

— Как называется этот ток?

IV. Закрепление новых знаний.

ЗАДАЧА: Определите мощность Р отдаваемую нагревательным элементом, имеющим сопротивление R и включенным в цепь источника тока с ЭДС ε и внутренним сопротивлением r. Каким должно быть внешнее сопротивление R, чтобы отдаваемая элементом мощность была наибольшей?

Учитель математики:

Большую часть своих усилий человек тратит на поиск наилучшего, оптимального решения поставленной задачи:

— как добиться наиболее высокого жизненного уровня;

— наивысшей производительности труда;

— наименьших потерь;

— максимальной прибыли;

— минимальных затрат времени.

Часть таких задач удаётся решить с помощью математического анализа.

— Откройте учебник на странице 151.Найдите схему применения метода поиска наибольших и наименьших значений функции к решению прикладных задач. Повторим основные этапы:

1) задача «переводится» на язык функций. Для этого выбирают удобный параметр х, через который интересующую нас величину выражают как функцию f(х);

2) средствами анализа ищется наибольшее или наименьшее значение этой функции на некотором промежутке;

3) выясняется, какой практический смысл( в терминах первоначальной задачи) имеет полученный(на языке функций) результат.

— Вернёмся к решению нашей задачи и применим к ней метод математического моделирования.

(один ученик решает задачу у доски).

Ответ: Мощность Р максимальна, когда внешнее сопротивление резистора равно внутреннему сопротивлению.

Учитель физики:

— Не только для определения электрических величин можно использовать математику. На территории нашего района находится сырзавод в с. Тугузтемир. Возможно, кому-то придётся заниматься переработкой молочных продуктов. Так вот

ЗАДАЧА: Сыроделы считают, что при равном объёме сыры шаровой формы лучше сохраняют свои вкусовые качества, чем сыры формы цилиндра и формы  прямоугольного параллелепипеда. Почему?

— Как может качество сыра зависеть от его формы?

— От каких факторов зависит испарение?

— Какова математическая модель данной практической задачи?

Учитель математики:

— Чтобы ответить на этот вопрос задачу можно сформулировать на языке геометрии:

ЗАДАЧА: Сравнить площади поверхностей прямоугольного параллелепипеда, цилиндра и шара, у которых одинаковые объёмы.

— Рассмотрим куб, цилиндр ,высота которого равна диаметру (или 2R) и шар.

В любом справочнике можно найти формулы, по которым вычисляются площади поверхностей и объёмы этих тел. Мы будем знакомиться с ними позже.

(На доске помещаются нужные формулы. Три ученика выходят к доске решать задачу.)

— Выразить через объём площадь поверхности:

а) куба; б) цилиндра; в) шара.

а)

б)

в)

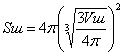
Sш < Sц < Sк

Ответ: вкусовые качества сыра шарообразной формы сохраняются дольше и лучше сыров другой формы.

V. Задание на дом:(тексты раздаются каждому ученику)

ЗАДАЧА: Батарея с ЭДС 12В и внутренним сопротивлением 0,8 Ом питает поочерёдно внешние цепи, имеющие сопротивления 0,4; 0,8 и 0,2 Ом. В каком случае полезная мощность наибольшая? Определите КПД батареи. Когда он наибольший? (УКАЗАНИЕ: используйте решение классной задачи.)

№ 321(учебник Алгебра и начала анализа , стр 154) –по желанию.

VI.Подведение итогов урока: