 Государственное бюджетное образовательное учреждение
Государственное бюджетное образовательное учреждение
среднего профессионального образования
Пермский политехнический колледж имени Н.Г. Славянова
Учебное занятие
Численные методы интегрирования
Пермь 2015
Цели занятия:
образовательные:
способствовать развитию мыслительных операций: аналогия, систематизация, обобщение, наблюдение;
формировать умения применять математические знания в практических задачах;
способствовать поддержанию интереса к предметам математики;
формировать умения трудиться;
помочь осознать роль знаний в жизни и обучении;
стимулировать самостоятельность;
работать в коллективе и в команде, эффективно общаться с коллегами, руководством, потребителями.
воспитательные:
научиться работать в микрогруппе;
научиться принимать чужую точку зрения и отстаивать свою;
научиться слушать своих товарищей;
научиться защищать решение задачи.
Задачи занятия:
познакомить с различными способами расчёта
выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество
осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач
Ход учебного занятия
Организационный момент
Основная задача дифференциального исчисления заключается в следующем: дана функция  , требуется найти ее производную. При этом если производная существует в каждой точке
, требуется найти ее производную. При этом если производная существует в каждой точке 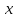 некоторого промежутка
некоторого промежутка 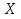 , то это также некоторая функция
, то это также некоторая функция  на
на 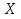 такая, что
такая, что  . Однако часто приходится решать и обратную задачу. Для решения обратной задачи служит операция интегрирования.
. Однако часто приходится решать и обратную задачу. Для решения обратной задачи служит операция интегрирования.
Проект носит прикладной характер (практико-ориентированный).
Объяснение нового материала
Постановка целей и задач занятия
Постановка проблемы
Как вычислить определенный интеграл от функций, первообразные которых выражаются через элементарные функции очень сложно, что требует большой вычислительной работы и с практической точки зрения не рационально? Как решать прикладные задачи, используя правила приближенного численного интегрирования, в которых необходимо находить интегралы не только от функций, заданных формулами, но и от функций, заданных табличным способом?
Итогом работы будет сравнение результатов вычисления определенных интегралов различными способами и оценка погрешности этих вычислений.
Гипотеза: предположим, что различными методами численного интегрирования можно вычислять определенные интегралы сравнительно легко и решать прикладные задачи с небольшой погрешностью .
Организация деятельности
Предполагается, проводить работу 3-мя группами.
1-я группа – работает над формулой приближенного интегрирования — формулой прямоугольников
виды работ
Подобрать и изучить литературу по данной теме
Проконсультироваться с преподавателями по данным вопросам
Составить математическую модель прикладной задачи
2-я группа – работает над формулой приближенного интегрирования – формулой трапеций
виды работ
Подобрать и изучить литературу по данной теме
Проконсультироваться с преподавателями по данным вопросам
Составить математическую модель прикладной задачи
3-я группа – работает над формулой приближенного интегрирования – формулой параболических трапеций ( формула Симпсона)
виды работ
Подобрать и изучить литературу по данной теме
Проконсультироваться с преподавателями по данным вопросам
Составить математическую модель прикладной задачи
Описание
Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам. Но вычислить интеграл непосредственным интегрированием удается далеко не всегда, а иногда это связано с большими трудностями. В этих случаях вычисление определенного интеграла по формуле Ньютона – Лейбница либо невозможно, либо затруднительно, поэтому прибегают к различным методам приближенного интегрирования.
Вычислить интеграл точно по формуле Ньютона – Лейбница с целью оценки погрешности при приближенном вычислении этого же интеграла.
Все три группы одновременно вычисляют интеграл :
Пример 1
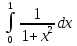 =
= 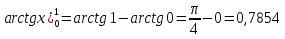 .
.
Блок 1
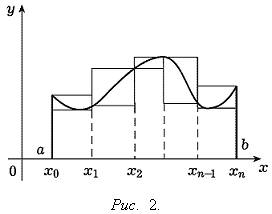
Разделим интервал интегрирования  на
на 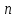 равных частей (частичных интервалов) и заменим данную трапецию ступенчатой фигурой, состоящей из
равных частей (частичных интервалов) и заменим данную трапецию ступенчатой фигурой, состоящей из 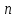 прямоугольников, опирающихся на частичные интервалы, причем высоты этих прямоугольников равны значениям функции
прямоугольников, опирающихся на частичные интервалы, причем высоты этих прямоугольников равны значениям функции 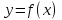 в начальных или конечных точках частичных интервалов. Значение площади этой фигуры и будет давать приближенное значение искомого интеграла
в начальных или конечных точках частичных интервалов. Значение площади этой фигуры и будет давать приближенное значение искомого интеграла 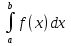 .
.
Если обозначить значения функции  в точках деления через
в точках деления через 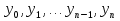 , то будем иметь следующую формулу — формулу прямоугольников :
, то будем иметь следующую формулу — формулу прямоугольников :
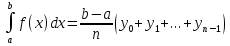
или
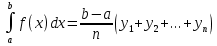
Блок 2
Оставим разбиение интервала  прежним, но заменим теперь каждую дугу линии
прежним, но заменим теперь каждую дугу линии 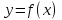 , соответствующую частичному интервалу . хордой, соединяющей конечные точки этой дуги. Таким образом, заменяем данную криволинейную трапецию
, соответствующую частичному интервалу . хордой, соединяющей конечные точки этой дуги. Таким образом, заменяем данную криволинейную трапецию 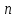 прямолинейными. Площадь каждой трапеции, построенной на частичном интервале, равна полусумме площадей , соответствующих этому интервалу прямоугольников. Суммируя все эти площади, получим формулу трапеций :
прямолинейными. Площадь каждой трапеции, построенной на частичном интервале, равна полусумме площадей , соответствующих этому интервалу прямоугольников. Суммируя все эти площади, получим формулу трапеций :

Блок 3
Разобьем интервал  на
на 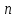 равных частей , но предположим, что
равных частей , но предположим, что 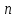 – четное число:
– четное число: 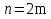 . Заменим дугу линии
. Заменим дугу линии 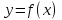 , соответствующую интервалу
, соответствующую интервалу  , дугой параболы, ось которой параллельна оси ординат и которая проходит через следующие три точки дуги: начальную точку дуги
, дугой параболы, ось которой параллельна оси ординат и которая проходит через следующие три точки дуги: начальную точку дуги 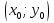 , среднюю точку
, среднюю точку  , конечную точку
, конечную точку 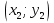 . Площадь данной трапеции приближенно равна сумме площадей получающихся параболических трапеций и выражается формулой :
. Площадь данной трапеции приближенно равна сумме площадей получающихся параболических трапеций и выражается формулой :
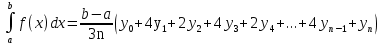
1 группа
Решает пример 1 по формуле прямоугольников : при 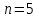
Таблица расчетов :
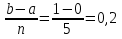
|
| 1 | 2 | 3 | 4 | 5 | |
|
|
| .2 | 0.4 | 0.6 | 0.8 | 1 |
|
| 1 | 0,9615 | 0,8621 | 0,7353 | 0,6098 | 0,5 |

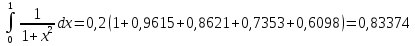
2 группа
Решает пример 1 по формуле трапеций : при 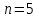
Таблица расчетов :
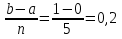
|
| 1 | 2 | 3 | 4 | 5 | |
|
|
| .2 | 0.4 | 0.6 | 0.8 | 1 |
|
| 1 | 0,9615 | 0,8621 | 0,7353 | 0,6098 | 0,5 |
3 группа
Решает пример 1 по формуле параболических трапеций : при 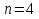
Таблица расчетов :

|
| 1 | 2 | 3 | 4 | |
|
|
|
|
|
|
|
|
| 1 |
|
|
|
|

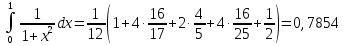
Занесем итоги расчета в таблицу и сравним:
| значение интеграла | абсолютная погрешность | относительная погрешность | |
| формула Н-Л | 0,7854 |
|
|
| фор-ла прям-ков | 0,8337 |
| 6,1 % |
| фор-ла трапеций | 0,7837 |
|
|
| фор-ла Симпсона | 0,7854 |
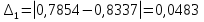
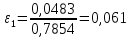 = 6,1 %
= 6,1 %
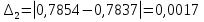
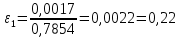
Вывод : гипотеза о том, что с помощью формул численного интегрирования можно вычислять определенные интегралы подтвердилась. Однако, при одном и том же значении 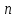 формула Симпсона дает лучшее приближение.
формула Симпсона дает лучшее приближение.
Пример 2
Вычислить определенный интеграл по формуле Симпсона с точностью до 0,0001
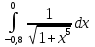
1 группа вычисляет интеграл при 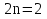
Вычислить шаг : 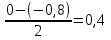
Расчетная таблица :
|
| 1 | 2 | |
|
| -0,8 | -0,4 |
|
|
| 0,61172 | 0,57833 | 0,57735 |
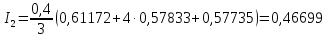
2 группа вычисляет интеграл при 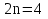
Вычислить шаг : 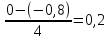
Расчетная таблица :
| 1 | 2 | 3 | 4 | ||
|
| -0,8 | -0,6 | -0,4 | -0,2 | |
|
| 0,611724 | 0,584981 | 0,578338 | 0,577381 | 0,57735 |
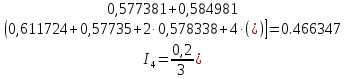
Оценим погрешность :
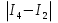 =
= 
3 группа 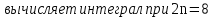
Вычислить шаг : 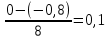
Расчетная таблица :
|
|
|
|
|
| |
| -0,8 | 0,611724 | 5 | -0,3 | 0,577584 | |
| 1 | -0,7 | 0,594236 | 6 | -0,2 | 0,577381 |
| 2 | -0,6 | 0.584981 | 7 | -0,1 | 0,577351 |
| 3 | -0,5 | 0,589381 | 8 | 0,577350 | |
| 4 | -0,4 | 0,578338 |
|
|
|
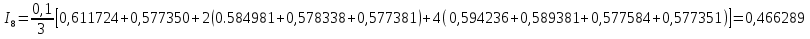
Оценим погрешность :
 =
= 
Полученная оценка погрешности меньше, чем требуемая точность.
Формула Симпсона дает практически точное вычисление определенного интеграла.
Приведенные правила численного интегрирования помогают решать прикладные задачи.
Прикладная задача
Ширина реки равна 20м; промеры глубины в некотором поперечном ее сечении через каждые 2м дали следующую таблицу :
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | ||
|
| 0.2 | 0,5 | 0,9 | 1,1 | 1,3 | 1,7 | 2,1 | 1,5 | 1,1 | 0,6 | 0,2 |
Расстояние (в метрах) от одного из берегов обозначено через 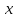 , соответствующая глубина реки ( также в метрах) – через
, соответствующая глубина реки ( также в метрах) – через  Требуется найти площадь
Требуется найти площадь 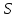 поперечного сечения реки.
поперечного сечения реки.
По формуле Симпсона находим :
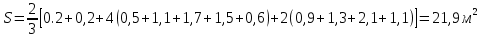
Представление результатов и их оценка
Самостоятельная работа студентов:
Вариант 1
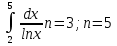
Вариант 2
Вариант 3

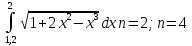
Вариант 4

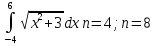
Вариант 5
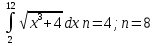
Литература
Пахомова Н.Ю. Метод учебного проекта в образовательном учреждении : Пособие для учителей и студентов пед.вузов, — М:АРКТИ, 2005г.
Чечель И.Д Исследовательский проекты в практике обучения. «Практика административной работы в школе» , 6/2003 г.
Богомолов Н.В. практические задания по математике. М.:Высшая школа 1990.
Бермант А. Ф., Араманович И. Г. Краткий курс математического анализа для втузов. — М.: Наука, 1967.
