Математическая копилка задач по комбинаторике

Краевое государственное общеобразовательное автономное учреждение

«Краевая общеобразовательная школа-интернат среднего (полного) общего образования по работе с одарёнными детьми

«ШКОЛА КОСМОНАВТИКИ»

Составили:

Зинкевич Алёна Ивановна, учитель математики

Халяк Татьяна Станиславовна, учитель математики

Содержание

1. Историческая справка. 4

2. Задачи на применение основных правил 6

   1. Правила суммы и произведения. 6

   2. Перестановки, перемещения, сочетания. 22

   3. Перестановки с повторениями, перемещения с повторениями, сочетания с повторениями. 44

3. Задачи повышенной трудности. 62

4. Методические рекомендации учителю. 73

5. Библиографический список. 74

1. Историческая справка

Представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов. Начальнику цеха надо распределить несколько видов работ между имеющимися станками, агроному – разместить посевы сельскохозяйственных культур на нескольких полях, заведующему учебной частью школы – составить расписание уроков, ученому-химику – рассмотреть возможные связи между атомами и молекулами, лингвисту – учесть различные варианты значений букв незнакомого языка и т.д. Область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов, называется комбинаторикой.

Комбинаторика возникла в XVI веке. В жизни привилегированных слоев тогдашнего общества большое место занимали азартные игры. В карты и кости выигрывались и проигрывались золото и бриллианты, дворцы и имения, породистые кони и дорогие украшения. Широко были распространены всевозможные лотереи. Понятно, что первоначально комбинаторные задачи касались в основном азартных игр – вопросов, сколькими способами можно выбросить данное число очков, бросая две или три кости, или сколькими способами можно получить двух королей в данной карточной игре. Эти и другие проблемы азартных игр явились движущей силой в развитии комбинаторики и развивающейся одновременно с теорией вероятностей.

Одним из первых занялся подсчетом числа различных комбинаций при игре в кости итальянский математик Тарталья. Он составил таблицу, показывавшую, сколькими способами могут выпасть r костей. Однако при этом не учитывалось, что одна и та же сумма очков может быть получена разными способами (например, 1+3+4=4+2+2).

Теоретическое исследование вопросов комбинаторики предприняли в XVII веке французские ученые Паскаль и Ферма. Исходным пунктом их исследования тоже были проблемы азартных игр. Особенно большую роль сыграла здесь задача о разделе ставки, которую предложил Паскалю его друг шевалье де Мере, страстный игрок. Проблема состояла в следующем: «матч» в орлянку ведется до шести выигранных партий; он был прерван, когда один игрок выиграл 5 партий, а другой – 4; как разделить ставку? Было ясно, что раздел в отношении 5:4 несправедлив. Применив методы комбинаторики, Паскаль решил задачу в общем случае, когда одному игроку остается до выигрыша r партий, а второму s партий. Другое решение задачи дал Ферма.

Дальнейшее развитие комбинаторики связано с именами Якова Бернулли, Лейбница и Эйлера. Однако и у них основную роль играли приложения к различным играм (лото, солитер и др.). За последние годы комбинаторика переживает период бурного развития, связанного с общим повышением интереса к проблемам дискретной математики. Комбинаторные методы используются для решения транспортных задач, в частности задач по составлению расписаний; для составления планов производства и реализации продукции. Установлены связи между комбинаторикой и задачами линейного программирования, статистики и т.д. Комбинаторика используется для составления и декодирования шифров и для решения других проблем теории информации.

Значительную роль комбинаторные методы играют и в чисто математических вопросах – теории групп и их представлений, изучении оснований геометрии, неассоциативных алгебр и т.д.

2. Задачи на применение основных правил

а) Правила суммы и произведения

Задача 1.

«В распоряжении сигнальщика есть 4 различных флага. На флагштоке поднимается сигнал, состоящий не менее, чем из двух флагов. Сколько различных сигналов можно поднять на флагштоке, если порядок флагов в сигнале учитывается?»

Решение.

Пусть A₁ – множество пар флагов, которое можно образовать из имеющихся четырех (с учетом порядка расположения флагов в паре). A₂ – множество таких троек, A₃ – множество таких четверок. Подсчитаем число элементов в каждом множестве. Рассмотрим A₁. 1-е действие – выбрать один флаг на первое место в паре, его можно осуществить 4 способами, так как всего 4 флага. 2-е действие – выбрать один флаг на второе место в паре, так как один флаг уже выбран (для расположения на первом месте в паре), то 2-е действие можно осуществить 4-1=3 способами. Следовательно, по правилу умножения, число элементов в множестве A₁ равно 43=12.

Аналогично находим, что A₂ образовано 432=24 элементами, а A₃ – 4321=24 элементами.

По условию, мы должны поднять только один сигнал, а значит, поднять только какие-либо два или только какие-либо три или только, наконец, какие-либо четыре флага. Тогда, пользуясь правилом суммы, находим искомое число сигналов: 12+24+24=60.

Ответ: 60 сигналов.

Задача 2.

«В классе изучают 10 предметов. Во вторник пять уроков, причем уроки разные. Сколькими способами можно составить расписание на вторник?»

Решение.

Присвоим условно всем десяти изучаемым предметам номера 1, 2,…, 10. пусть 1-е действие – поставить в расписание какой-либо изучаемый предмет первым уроком, 2-е действие – поставить в расписание какой-либо предмет вторым уроком, …, 5-е действие – поставить в расписание какой-либо изучаемый предмет пятым уроком. 1-е действие, очевидно, можно осуществить десятью способами (так как любой из 10 изучаемых предметов можно поставить в расписание первым уроком), 2-е действие можно осуществить девятью способами (т.к. один из 10 предметов уже поставлен в расписание первым уроком), 3-е действие можно осуществить восемью способами (т.к. уже два предмета поставлены в расписание первым и вторым уроками), …, 5-е действие можно осуществить шестью способами. Следовательно, по принципу умножения, все пять действий можно осуществить 109876=30240 способами, т.е. число способов составить расписание на вторник равно 30 240.

Ответ: 30240 способов.

Задача 3.

«В студенческой группе обучаются 16 юношей и 15 девушек. Сколькими способами можно избрать старосту группы (либо юношу, либо девушку), если любой студент группы может быть избран на эту должность?»

Решение.

По правилу суммы выбор старосты группы можно осуществить 16+15=31 способами.

Ответ: 31 способом.

Задача 4.

Команда космического корабля

В случае, когда число возможных выборов на каждом шагу зависит от того, какие элементы были выбраны ранее, удобно изображать процесс составления комбинаций в виде «дерева». Сначала из одной точки проводят столько отрезков, сколько различных выборов можно сделать на первом шагу (таким образом, каждый отрезок соответствует одному элементу). Из конца каждого отрезка проводят столько отрезков, сколько можно сделать выборов на втором шагу, если в первый раз был выбран данный элемент и т. д.

В результате такого построения получается «дерево», рассмотрение которого легко дает число решений нашей задачи.

Р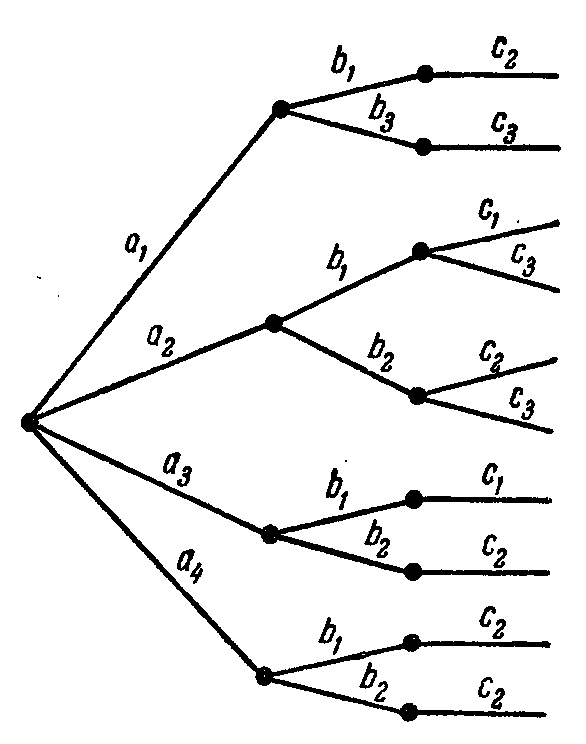ассмотрим следующий пример. Известно, что при составлении команд многоместных космических кораблей возникает вопрос о психологической совместимости участников космического путешествия. Даже вполне под ходящие порознь люди могут оказаться непригодными для длительного совместного путешествия. Предположим, что надо составить команду космического корабля из трех человек: командира, инженера и врача. На место командира есть четыре кандидата a₁, а₂, а₃, a₄, на место инженера — 3 кандидата b₁, b₂,b₃ и на место врача — 3 кандидата с₁ с₂, с₃. Проведенная проверка показала, что командир а₄ психологически совместим с инженерами b₁, b₃ и врачами с₁, с₃,, командир а₂ с инженерами b₁ и b₂ и всеми врачами, командир а₃ — с инженерами b₁ и b₂ и врачами с₁ c₃, командир a₄ — со все ми инженерами и врачом с₂. Кроме того, инженер b₁ психологически несовместим с врачом с₂, инженер b₂ — с врачом с₁ и инженер b₃—с врачом c₂. Сколькими способами при этих условиях может быть составлена команда корабля?

Соответствующее дерево изображено на рис. 2.

Оно показывает, что есть лишь 10 допустимых комбинаций (если бы не было ограничения совместимости, то число комбинаций по правилу произведения равнялось бы 36=433).

Задача 5.

«Из горда А в город В ведут пять дорог, а из города В в город С – три дороги. Сколько путей, проходящих через В, ведут из А в С?»

Замечание. Очень часто правило произведения формулируют в несколько иной форме. Если интерпретировать выбор элемента из множества А₁ как некоторое первое действие, выбор элемента из А₂ – как второе действие и так далее, выбор элемента из множества А_k – как k-ое действие, то теорему можно сформулировать в следующей форме.

Теорема: «Пусть необходимо выполнить одно за другим k действий. Если первое действие можно выполнить n₂ способами, после чего третье действие можно выполнить n₃ способами, и т.д. до k-го действия, которое можно выполнить n_k, то все k действия вместе можно выполнить (в указанном порядке) способами».

Решение.

1-й способ. Пусть А₁ – множество, элементами которого являются дороги, ведущие из А в В, А₂ – множество, элементами которого являются дороги, ведущие из В в С. Ясно, что путь из А в С, проходящий через В, — это пара (a₁,a₂)(пара дорог), где a₁  A_1, a₂  A₂. по теореме, число таких пар (то есть фактически число путей из А в В, проходящих через В) равно 5*3=15.

2-й способ. 1-е действие – переезд из А в В, 2-е действие – переезд из В в С. Первое действие можно осуществить (выполнить) пятью способами, 2-е действие – тремя способами. Последовательное выполнение 1-го и 2-го действий – это путь (переезд) из А в С через В. Отсюда следует, что по принципу умножения (в той формулировке, которая приведена в замечании) искомое число путей равно 5*3=15.

Ответ: 15 способов.

Задача 6.

«Сколько трехзначных чисел можно составить из цифр 1, 3, 5, если цифры в числе не повторяются?»

Решение.

На месте сотен поставим любую из трех цифр. После каждого такого выбора на месте десятков можно поставить любую из двух оставшихся цифр, так как цифры в числе не повторяются. Наконец, на месте единиц можно поставить оставшуюся одну цифру. Повторным применением правила произведения найдем число трехзначное чисел, равное N=3*2*1=6.

Г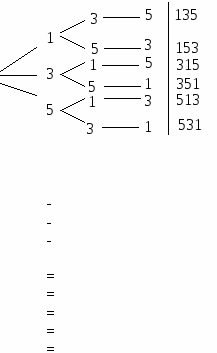рафической иллюстрацией является специальный граф, называемый «деревом».

Начало

Задача 7.

«В кухне пять лампочек. Сколько существует способов освещения?»

Примечание. Под способами освещения подразумевается то, что каждая лампа может гореть и не гореть. Два способа считаются различными, если они отличаются состоянием хотя бы одной лампы.

Решение.

Первый способ. Число способов освещения, при которых горит одна лампа из пяти, равно числу способов освещения, при которых горят 4 лампы из пяти (рис.1).

Рис.1

Рис.2

Рис.3

Аналогично, число способов освещения, при которых горят 2 лампы из пяти, равно числу способов, при которых не горят 2 лампы из пяти (т.е. горят 3 лампы из пяти). Эти способы показаны на рис.2 (10 способов, при которых горят 2 лампы, и 10 способов, при которых горят 3 лампы). Имеются еще два способа (рис.3) (все лампы горят, все лампы не горят). Мы перебрали все способы освещения и теперь их легко сосчитать.

Второй способ. 1) Пусть в кухне имеется одна лампа. Она может быть в двух состояниях: не гореть ● или гореть○, т.е. способов освещения 2.

2) 2 лампы. Первая лампа может быть в двух состояниях: ● и ○. Каждое из них можно скомбинировать с любым из двух состояний второй лампы: если вторая лампа не горит, получаем 2 способа освещения (рис.4).

Рис.4

Рис.5

Рис.6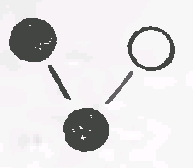

Если вторая лампа горит, получаем еще 2 способа (рис.5). Всего способов освещения 4 (рис.6).

3) 3 лампы. Первые две лампы могут быть в четырех состояниях. Каждое из этих четырех состояний можно скомбинировать с любым из двух состояний третьей лампы (рис.7).

Рис.7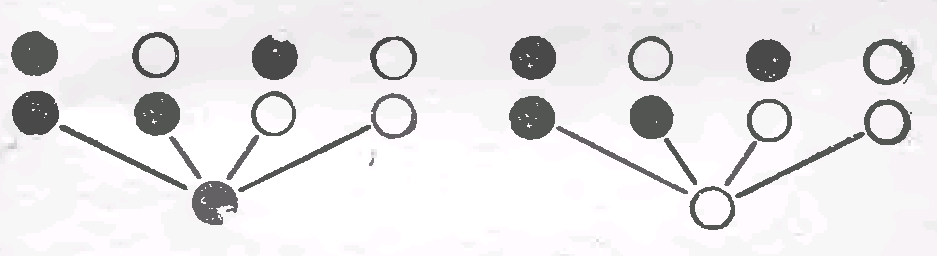

Всего способов освещения 8 (рис.8).

Рис.8

4) 4 лампы. Первые три лампы могут быть в восьми состояниях. Каждое из них можно скомбинировать с любым из двух состояний четвертой лампы. Имеется 82=16 способов освещения.

5) 5 ламп. Имеется 162=32 способа освещения. Рассмотренный метод решения допускает незначительные модификации; переход от двух ламп к трем можно иллюстрировать не только приведенной выше схемой, но и следующими схемами (рис.9).

Рис.9

Обе они тоже показывают, что добавление одной лампы (которая может быть в двух состояниях) увеличивает число способов освещения вдвое.

Ответ: 25 способов.

Задача 8.

О домино

Сколькими способами из 28 костей домино можно выбрать две кости так, чтобы их можно было приложить друг к другу (то есть чтобы какое-то число очков встречалось на обеих костях)?

Решение.

Сначала выберем одну кость. Это можно сделать 28 способами. При этом в 7 случаях выбранная кость окажется «дублем», то есть костью вида 00, 11, 22, 33, 44, 55, 66, а в 21 случае — костью с различными числами очков (например, 05, 13 и т. д.). В первом случае вторую кость можно выбрать 6 способами (например, если на первом шагу выбрана кость 11, то на втором шагу можно взять одну из костей 01, 12, 13, 14, 15, 16). Во втором же случае вторую кость можно выбирать 12 способами (для кости 35 подойдут кости 03, 13, 23, 33, 34, 36, 05, 15, 25, 45, 55, 56). По правилу произведения в первом случае получаем 76=42 выбора, а во втором 2112 = 252 выбора. Значит, по правилу суммы получаем 42+252 = 294 способов выбора пары.

В проведенном рассуждении учитывался и порядок, в котором выбирались кости. Поэтому каждая пара костей появлялась дважды (например, первый раз 01 и 16, а второй раз 16 и 01). Если не учитывать порядок выбора костей, то получим вдвое меньше способов выбора, то есть 147 способов.

Ответ: 147 способов.

Задача 9.

«Какое наибольшее число слонов можно расставить на шахматной доске так, чтобы они не угрожали друг другу? Доказать, что число способов такой расстановки слонов есть квадрат некоторого числа.»

Рис.10

Рис.11

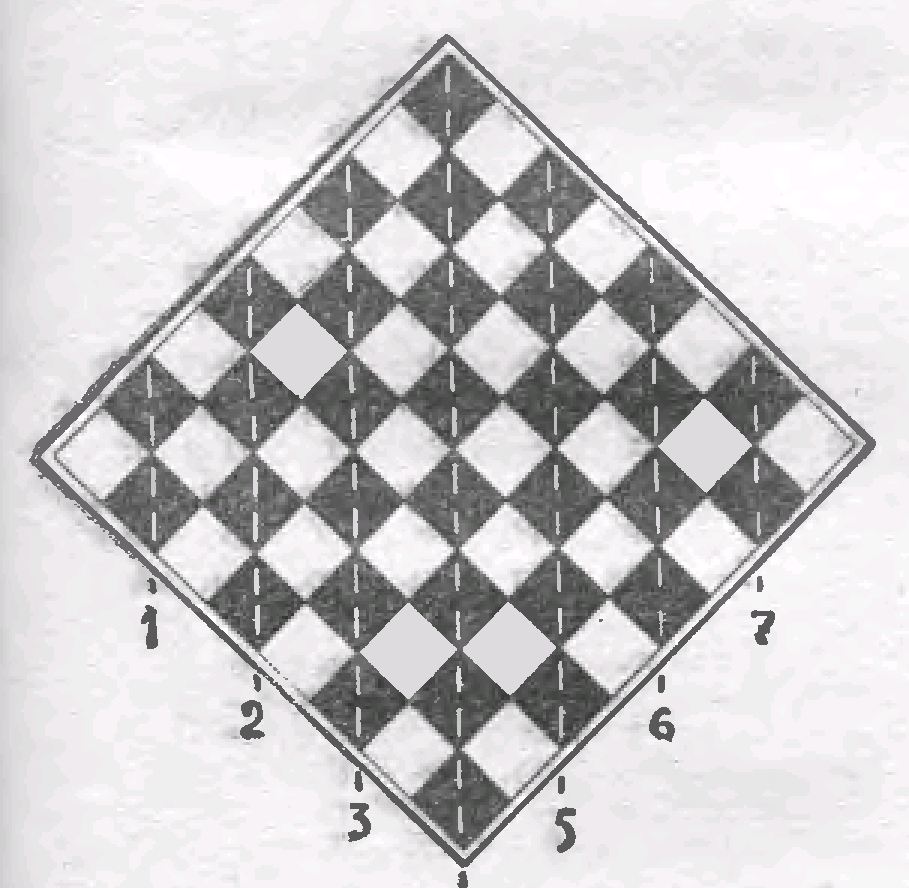
Примечание. Чтобы понять условие, нужно, конечно, знать, как ходит слон. Слон ходит по диагоналям. Например, с поля d3 слон одним ходом может попасть на любое из полей, отмеченных на рис.10 (b1, с2 и т. д.). Таким образом, 2 слона угрожают друг другу, если они стоят на одной диагонали.

Решение.

В указании к задаче показан конкретный пример расстановки 14 слонов. Следовательно, 14 слонов расставить можно. Если мы докажем, что больше чем 14 слонов расставить нельзя, то первая половина задачи будет решена.

Рассмотрим сначала чернопольных слонов. Сколько их можно расставить на шахматной доске, чтобы они не угрожали друг другу? 7 поставить можно; докажем, что нельзя поставить больше.

Выберем 7 черных диагоналей, параллельных друг другу (рис.11). На одной диагонали может стоять максимум одни слон. Поэтому ответ: 7. Если мы возьмем «черные» диагонали, перпендикулярные указанным, то их окажется 8 (причем крайние будут содержать по одной клетке). Рассматривая эти диагонали, тоже можно было бы убедиться, что больше семи слонов поставить нельзя (действительно, если поставлено восемь слонов, не бьющих друг друга, то два из них должны оказаться на крайних диагоналях, но так как каждая из этих диагоналей состоит из одной клетки, то эти два слона должны оказаться в противоположных углах доски, т.е. бить друг друга). Но это рассуждение излишне, так как мы получаем наш результат более простым способом, выбрав диагонали, как указано на рис.11.

Максимальное число белопольных слонов, не угрожающих друг другу, тоже равно 7. Белопольный и чернопольный слоны не могут угрожать друг другу. Значит, всего на доске можно расставить максимум 14 слонов, не угрожающих друг другу.

Обозначим через Б число способов расставить 7 белопольных слонов, не угрожающих друг другу; через Ч – число способов расставить 7 чернопольных слонов, не угрожающих друг другу; наконец, через С – число способов расставить 14 слонов, не угрожающих друг другу. Ясно, что Б=Ч, C=БЧ=(Ч)²,т.е. С – квадрат некоторого числа.

Ответ: 14 слонов.

Задача 10.

«Из Киева до Чернигова можно добраться пароходом, поездом, автобусом, самолетом; из Чернигова до Новгорода-Северского – пароходом и автобусом. Сколькими способами можно осуществить путешествие по маршруту Киев–Чернигов–Новгород-Северский?»

Решение.

Очевидно, число разных путей из Киева до Новгорода-Северского равно 42=8, так как, выбрав один из четырех возможных способов путешествия от Киева до Чернигова, имеем два возможных способа путешествия от Чернигова до Новгорода-Северского (рис.14).

Рис.14

Ответ: 8 способов.

Задача 11.

«В розыгрыше первенства страны по футболу принимает участие 16 команд. Сколькими способами могут быть распределены золотая и серебряная медали?»

Решение.

Золотую медаль может получить одна из 16 команд. После того как определен владелец золотой медали, серебряную медаль может иметь одна из 15 команд. Следовательно, общее число способов, которыми могут быть распределены золотая и серебряная медали, равно 1615=240.

Ответ: 240 способов.

Задача 12.

«Сколько чётных четырёхзначных чисел можно составить, используя лишь цифры 0,1,2?»

Примечание: При решении задачи использовали правило умножения: если A₁,A₂,…A_k содержит соответственно n₁,n₂,…,n_k элементов, то прямое произведение состоит из числа элементов.

Решение.

Первой цифрой можно взять 1 или 2, т.е. первая цифра может быть выбрана двумя способами. Для каждого из этих способов второй цифрой можно взять любую из трёх цифр: 0,1,2. Таким образом, получим 23 = 6 способов выбора первых двух цифр. Для каждого способа выбора первых двух цифр третью цифру можно выбрать тремя способами, а первые три цифры 63=18 способами. Для каждого из этих 18 способов четвёртую цифру можно выбрать двумя способами: 0 или 2, это вытекает из того, что по условию число должно быть чётным. Значит всего чётных четырёхзначных чисел, составленных из цифр 0, 1, 2, имеется 182 =36. Итак, учитывая, что 1-ая и 4-ая цифры могут быть выбраны 2 способами, а 2-ая и 3-ая тремя, количество всех искомых чисел получаем по правилу: 2332=36.

Ответ: 36

Задача 13.

«Сколько четырехзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, если:

а) ни одна из цифр не повторяется более одного раза;

б) цифры могут повторяться;

в) числа должны быть нечетными (цифры могут повторяться)?»

Решение.

а) Первой цифрой числа может быть одна из 5 цифр 1, 2, 3, 4, 5 (0 не может быть первой цифрой, потому что в таком случае число не четырехзначное); если первая цифра выбрана, то вторая может быть выбрана 5 способами, третья – 4 способами, четвертая – 3 способами. Согласно правилу умножения общее число способов равно 5543=300.

б) Первой цифрой может быть одна из цифр 1, 2, 3, 4, 5 (5 возможностей), для каждой из следующих цифр имеем 6 возможностей (0, 1, 2, 3, 4, 5). Следовательно, число искомых чисел равно 5666=56³=1080.

в) Первой цифрой может быть одна из цифр 1, 2, 3, 4, 5, а последней – одна из цифр 1, 3, 5 (числа должны быть нечетными). Следовательно, общее количество чисел равно 5663=540.

Ответ: 300, 1080, 540 способами.

b) Перестановки, сочетания, размещения

Задача 14.

Лингвистические проблемы

Лингвистам — специалистам по живым и мертвым языкам, часто приходится разгадывать надписи, сделанные на незнакомых языках. Предположим, что им попался текст, написанный при помощи 26 незнакомых знаков. Эти знаки являются буквами, изображающими каждый один из 26 звуков. Сколькими способами можно сопоставить звуки знакам письма?

Расположим знаки письма в некотором порядке. Тогда каждый способ сопоставления даст некоторую перестановку звуков. Но из 26 звуков можно составить Р₂₆=26! перестановок. А это число приблизительно равно 410²⁶. Разумеется, проверить все эти возможности непосильная работа не только для человека, но и для электронной вычислительной машины. Поэтому стараются уменьшить число возможностей. Часто удается отделить знаки, обозначающие гласные от знаков, обозначающих согласные (гласные чаще стоят рядом с согласными, чем гласные рядом с гласными или согласные рядом с согласными; наблюдая, какие сочетания знаков чаще всего встречаются, можно отделить знаки для гласных от знаков для согласных). Предположим, что удалось найти 7 знаков для гласных и 19 знаков для согласных. Подсчитаем, во сколько раз уменьши лось число возможностей?

7 знаков для гласных можно переставлять друг с другом 7! способами, а 19 знаков для согласных 19! способами. Общее число комбинаций равно 7!•19!. Значит, работа уменьшилась в 26!/7!•19!≈650000 раз. Конечно, стало легче, но и 7!19! — гигантское число.

Далее подсчитывают частоту появления отдельных знаков. Сравнивая эту частоту с частотой появления букв в близких к данному языках, можно примерно угадать значения некоторых знаков. Другие знаки удается найти, сравнив данный текст с тем же текстом на ином языке (древние цари любили вещать о своих «подвигах» на нескольких языках).

Предположим, что в результате этой работы опознано 4 гласных и 13 согласных букв. Сколько еще остается возможностей?

Ясно, что 3!•6! =4320. А такое число комбинаций уже можно по порядку проверить, используя электронные вычислительные машины.

Задача 15.

«На полке стоят 10 различных книг. Сколькими способами можно выбрать из них 3 книги?»

Решение.

Искомое число равно числу способов образовать 3-х элементные (неупорядоченные) подмножества из множества, содержащего 10 различных элементов, то есть равно

.

Ответ: 120 способов.

Задача 16.

«У мамы два яблока и три груши. Каждый день в течение пяти дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано?»

Решение.

Вот один способ раздать яблоки и груши: (в 1-й и 3-й день – яблоки, во 2-й, 4-й и 5-й дни – груши), вот еще один способ: (в первые три дня – груши, в последние два – яблоки). Итак, нужно пересчитать все таблички из двух светлых и трех темных кружков. Выполняя рассуждения, аналогичные задаче 1, получаем количество способов равно =10.

Ответ: 10 способов.

Задача 17.

«Сколькими способами можно расставить на шахматной доске 8 ладей так, чтобы они не били друг друга?»

Примечание. Ладья ходит по горизонталям и вертикалям. Например, ладья d3 угрожает всем полям вертикали d и горизонтали 3 (рис.12).

Рис.12

Решение.

Мы уже доказали, что на каждой вертикали стоит ровно одна ладья (см. указания). Разумеется, и на каждой горизонтали стоит тоже ровно одна ладья. Ладью на вертикаль а можно было поставить на любое из восьми полей (все горизонтали были свободны). Но после того, как эта ладья поставлена на доску, одна горизонталь уже занята (если, например, ладья стоит на поле а2, то на горизонталь 2 нельзя ставить другие ладьи). Поэтому на вертикаль b ладью можно поставить только семью способами. После того как и ладья b поставлена на доску, заняты уже 2 горизонтали, а свободных горизонталей остается 6, так что ладью с можно ставить на любое из 6 полей. Ладью d можно поставить пятью способами, ладью е – четырьмя, f – тремя, g – двумя, h – только одним. Итак, ладью а можно поставить на доску восемью способами. Число способов поставить на доску ладьи а и b равно 8*7. Число способов расстановки ладей а, b и с равно 8*7*6 и т.д. Ладьи а, b, с,…, h можно поставить на доску 8*7*6*5*4*3*2*1=8! способами.

Ответ: 8! способов.

Задача 18.

«Сколькими способами из n предметов можно выбрать два?»

Решение.

Перенумеруем n предметов: 1, 2, …, n. Теперь каждый способ выбрать 2 предмета из n соответствует паре чисел (номера выбранных предметов), причем пары (k,m) и (m,k), очевидно, определяют один и тот же способ. Итак, равно числу пар (1,2), (1,3), … , (n-1,n).

Первый номер в паре может принимать n значений, второй – остальные n-1 значений. Всего пар n(n-1). Но пары номеров (k,m) и (m,k) при этом сосчитаны обе, хотя они определяют одну и ту же пару предметов. Значит, .

Ответ: способов.

Задача 19.

«Сколько можно составить перестановок из n элементов, в которых данные два элемента не стоят рядом?»

Решение.

Определим число перестановок, в которых данные два элемента a и b стоят рядом, и вычтем это число из числа всех перестановок из n элементов. Как бы слепим элементы a и b, т.е., будем аb считать одним элементом, получим P_n-1 таких перестановок, столько же перестановок, в которых a и b, расположены в другом порядке: b*a. Следовательно, перестановок из n элементов, в которых данные два элемента не стоят рядом, P_n-2P_n-1.

Ответ: P_n-2P_n-1

Задача 20.

«У отца есть пять попарно различных апельсинов, которые он выдает своим восьми сыновьям так, что каждый получает либо один апельсин, либо ничего. Сколькими способами это может быть сделано?»

Решение.

Обозначим число способов раздать 5 попарно различных апельсинов восьми сыновьям через . Подсчитаем двумя методами.

Первый метод. Число способов выбрать из восьми сыновей пятерых (тех, которые получат апельсины) равно . Любому такому выбору соответствует 5! способов раздачи апельсинов (число способов раздать 5 попарно различных апельсинов пяти сыновьям). Значит, .

Второй метод. Первый апельсин можно дать любому из 8 сыновей. Второй – любому из оставшихся 7 сыновей и т.д. Пятый – любому из оставшихся 4 сыновей (остальные трое не получат апельсинов). Итак, .

Ответ: способов.

Задача 21.

Львы и тигры

Укротитель хищных зверей хочет вывести на арену цирка 5 львов и 4 тигров; при этом нельзя, чтобы два тигра шли друг за другом. Сколькими способами он может расположить зверей.

Решение.

Поставим сначала всех львов так, чтобы между каждыми двумя львами был промежуток. Это можно сделать 5!=120 способами. Число промежутков равно 4. Если присоединить к ним еще два места — впереди всех львов и позади них, то получится 6 мест, на которые можно поставить тигров, причем никакие два тигра не окажутся рядом друг с другом. Так как порядок тигров существен, то число способов их расстановки равно числу размещений из 6 по 4, то есть . Комбинируя каждый способ расстановки львов с одним из способов расстановки тигров, получаем 120360=43200 способов вывести хищных зверей на арену.

Если бы у дрессировщика было п львов и b тигров, то он мог бы решить задачу способами. Это возможно лишь при условии, что k  n+1 — иначе два тигра обязательно окажутся рядом.

Задача 22.

«Сколько диагоналей можно провести в выпуклом n-угольнике?»

Решение.

Возьмем все пары различных вершин многоугольника (таких пар ) и соединим отрезками точки каждой пары. Получим отрезков. Среди них будет n сторон, а остальные – диагонали, т.е. диагоналей будет .

Ответ: .

Задача 23.

«Сколькими способами читатель может выбрать 3 книжки из 5?»

Решение.

Искомое число способов равно числу трехэлементных подмножеств множества из 5 элементов: .

Ответ: 10 способов.

Задача 24.

Рыцари короля Артура

За круглым столом короля Артура сидят 12 рыцарей. Из них каждый враждует со своими соседями. Надо выбрать 5 рыцарей, чтобы освободить заколдованную принцессу. Сколькими способами это можно сделать так, чтобы среди выбранных рыцарей не было врагов?

Решение.

Рассмотрим случай, когда рыцари сидят в ряд.

Для этого возьмем какого-нибудь рыцаря, скажем, сэра Ланселота. Все выбираемые комбинации рыцарей распадаются на два класса — в одних из них участвует сэр Ланселот, а в других нет. Подсчитаем, сколько комбинаций входит в каждый класс.

Если сэр Ланселот отправляется освобождать заколдованную принцессу, то ни его сосед справа, ни его сосед слева уже не примут участия в этой экспедиции. Остаются 9 рыцарей, из которых надо выбрать 4 спутников для сэра Ланселота. Так как соседи Ланселота не участвуют в экспедиции, то надо лишь проследить, чтобы среди выбранных 4 рыцарей не было врагов, то есть, чтобы никакие два из них не сидели рядом. Но исключение сэра Ланселота и его двух соседей разрывает цепь рыцарей, и можно считать, что они сидят не за круглым столом, а в один ряд. А в этом случае вы брать 4 рыцарей из 9 требуемым образом можно способами. Итак, в первый класс входит 15 комбинаций.

Теперь сосчитаем, сколько комбинаций входит во второй класс.

Так как сэр Ланселот не участвует в экспедиции, то его можно сразу исключить из числа рыцарей круглого стола. А тогда цепь рыцарей и их взаимоотношений разрывается, и остаются 11 рыцарей, расположенных в ряд. Из них надо выбрать 5 участников экспедиции так, чтобы среди выбранных не было двух сидящих рядом. Это можно сделать способами. Таким образом, общее число способов равно 15 + 21=36.

Вообще, если за круглым столом сидят п рыцарей, и надо выбрать k рыцарей так, чтобы в их число не попали никакие два соседа, то это можно сделать способами.

Это утверждение доказывается точно так же, как и выше. Все комбинации рыцарей разбивают на два класса в зависимости от того, участвует или нет в них рыцарь Ланселот. Комбинаций, где он участвует, будет , а комбинаций, в которые он не входит, . Легко проверяется, что

Задача 25.

«В турнире принимали участие n шахматистов, и каждые 2 шахматиста встретились 1 раз. Сколько партий было сыграно в турнире?»

Решение.

Партий было сыграно столько, сколько можно выделить 2-элементных подмножеств в множестве из n элементов, т.е. .

Ответ: партий.

Задача 26.

«Сколькими способами можно упорядочить множество {1, 2, …, 2n} так, чтобы каждое четное число имело четный номер?»

Решение.

Четные числа можно расставить на местах с четными номерами (таких мест n) n! способами; каждому способу размещения четных чисел на местах с четными номерами соответствует n! способов размещения нечетных чисел на местах с нечетными номерами. Поэтому общее число перестановок указанного типа по правилу умножения равно n!n!=(n!)².

Ответ: (n!)² способов.

Задача 27.

«Учащемуся сдать 4 экзамена на протяжении 8 дней. Сколькими способами это можно будет сделать, если последний экзамен надо сдать на восьмой день?»

Решение.

Искомое число способов равно числу 4-элементных упорядоченных подмножеств (дни сдачи экзаменов) множества из 8 дней, т.е. Если известно, что последний экзамен будет сдаваться на восьмой день , то число способов равно ( в восьмой день любой из 4-х экзаменов, а 3 оставшихся экзамена в остальные дни)

Ответ: 840.

Задача 28.

«Сколькими способами можно составить шестицветный флаг из шести полос материала различного цвета?»

Решение.

Искомое число способов равно числу способов упорядочения множества из шести элементов, то есть равно P₆=6!=1*2*3*4*5*6=720.

Ответ: 720 способов.

Задача 29.

Хоровод

«Семь девушек водят хоровод. Сколькими различными способами они могут встать в круг?»

Решение.

Если бы они стояли на месте, то получилось бы 7! = 5040 перестановок. Но так как танцующие кружатся, то их положение относительно окружающих предметов не существенно, а важно лишь взаимное расположение. Поэтому перестановки, переходящие друг в друга при кружении танцовщиц надо считать одинаковыми. Но из каждой перестановки можно получить еще шесть новых путем вращения. Значит, число 5040 надо разделить на 7. Мы получаем 5040:7=720 различных перестановок девушек в хороводе.

Ответ: 720 перестановок.

Задача 30.

«В скольких точках пересекаются диагонали выпуклого n-угольника, если никакие 3 из них не пересекаются в одной точке?»

Решение.

Каждой точке пересечения двух диагоналей соответствует 4 вершины n-угольника, а каждым 4 вершинам n-угольника соответствует 1 точка пересечения (точка пересечения диагоналей четырехугольника с вершинами в данных 4 точках). Поэтому число всех точек пересечения равно числу способов, которыми среди n вершин можно выбрать 4 вершины: .

Ответ: в точках.

Задача 31.

«Рассмотрим прямоугольную сетку квадратов размерами mn («шахматный город», состоящий из mn прямоугольных кварталов, разделенных n-1 «горизонтальными» и m-1 «вертикальными» улицами (рис.15)). Каково число различных кратчайших путей на этой сетке, ведущих из левого нижнего угла (точки (0;0)) в правый верхний угол (точку (m;n))?»

Рис.14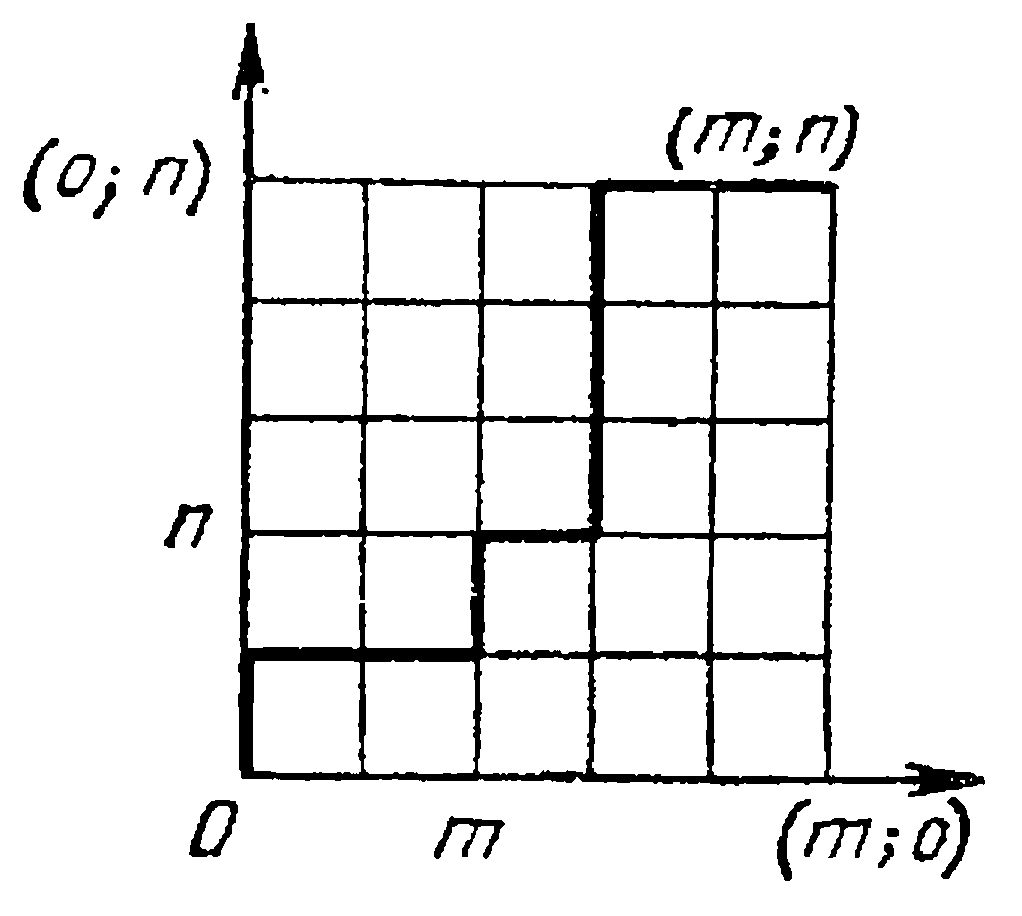

Решение.

Каждый кратчайший путь из точки (0;0) в точку (m;n) состоит из m+n отрезков, причем среди них есть m горизонтальных и n вертикальных отрезков. Разные пути отличаются лишь порядком чередования горизонтальных и вертикальных отрезков. Поэтому общее число путей равно числу способов, которыми из m+n отрезков можно выбрать n вертикальных отрезков, т.е. .

Ответ: кратчайших путей.

Задача 32

«Из двух математиков и десяти экономистов надо составить комиссию в составе 8 человек. Сколькими способами, может быть составлена комиссия, если в неё должен входить хотя бы один математик?»

Решение.

Комиссия может состоять либо из одного математика и семи экономистов, либо из двух математиков и шести экономистов. В первом случае получаем: одного математика из двух можно выбрать двумя способами, а 7 экономистов из 10 – способами (число 7-элементных подмножеств 10-тиэлементного подмножества), то число способов выбора комиссии из 1 математика и 7 экономистов равно 2. Если включить в комиссию обоих математиков, то 6 экономистов из 10 можно выбрать способами. Общее число способов выбора комиссии с одним или двумя математиками равно 2 + =

Примечание. При решении задачи использовано правило суммы: если элемент у можно выбрать m способами, а элемент y — n способами, причём ни один из способов выбора х не совпадает со способами y, то х или у можно осуществить m+n способами. (Если множество А содержит m элементов, а множество B – n элементов и А  В = , то АВ содержит m+n элементов.)

Рассмотрим другой способ решения задачи. Подсчитаем, сколькими способами можно выбрать из 12 человек комиссию в составе 8 человек (таких способов ) и вычтем из этого числа число комиссий, не содержащих ни одного математика. Комиссий, состоящих только из экономистов, можно составить . Следовательно, число комиссий, в которые входит хотя бы один математик равно .

Ответ: 450.

Задача 33

«Из колоды, содержащей 52 карты, вынули 10 карт. Сколькими различными способами это можно сделать? В скольких случаях среди этих карт окажется хотя бы один туз? Ровно 4 туза?»

Решение.

Выбрать 10 карт из 52 можно способами. Найти число способов, когда среди выбранных карт есть хотя бы один туз, на первый взгляд сложнее – надо разбирать случаи, когда есть ровно один туз, ровно два туза, ровно три туза, ровно 4 туза. Но проще найти сначала, в скольких случаях нет ни одного туза – во всех остальных случаях будет хотя бы один туз. Но если среди выбранных карт нет ни одного туза, то выбор совершался не из 52 карт, а из 48 карт (всех кроме тузов), а поэтому число таких выборов равно . Следовательно, хотя бы один туз будет в — случаях. Подсчитаем, в скольких случаях будет ровно один туз. Т.к. один туз можно выбрать из 4-х тузов четырьмя способами, а из оставшихся 48 карт выбрать остальные 9 можно способами, то ровно один туз в 4. И наконец, выбор, содержащий все 4 туза, можно сделать способами – надо взять 4 туза и выбрать ещё 6 карт из 48.

Ответ: , — , 4,

c) Перестановки, сочетания, размещения (с повторениями)

Задача 34.

Суеверные велосипедисты

«Опять восьмерка!» — горестно воскликнул председатель клуба велосипедистов, взглянув на погнутое колесо своего велосипеда. «А все почему? Да потому, что при вступлении в клуб мне выдали билет за номером 008. И теперь месяца не проходит, чтобы то на одном, то па другом колесе не появилась восьмерка. Надо менять номер билета. А чтобы меня не обвиняли в суеверии, проведу-ка я перерегистрацию всех членов клуба и буду, выдавать только билеты с номерами, в которые ни одна восьмерка не входит».

Сказано — сделано, и на другой день он заменил все билеты. Сколько членов было в клубе, если известно, что использованы все трехзначные номера, не содержащие ни одной восьмерки? (Например, 000 использован, а 836 нет.)

Решение.

Определим сначала, сколько однозначных номеров не содержит восьмерку.

Ясно, что таких номеров девять 0, 1, 2, 3, 4, 5, 6, 7, 9 (номер 8 пропускается). А теперь найдем все двузначные номера, не содержащие восьмерок. Их можно составить так: взять любой из найденных однозначных номеров и написать после него любую из девяти допустимых цифр. В результате из каждого однозначного номера получится девять двузначных. А так как однозначных номеров тоже 9, то получится 99=81 двузначный номер без восьмерок. Вот они:

00, 01, 02, 03, 04, 05, 06, 07, 09

10, 11, 12, 13, 14, 15, 16, 17, 19

20, 21, 22, 23, 24, 25, 26, 27, 29

30, 31, 32, 33, 34, 35, 36, 37, 39

40, 41, 42, 43, 44, 45, 46, 47, 49

50, 51, 52, 53, 54, 55, 56, 57, 59

60, 61, 62, 63, 64, 65, 66, 67, 69

70, 71, 72, 73, 74, 75, 76, 77, 79

90, 91, 92, 93, 94, 95, 96, 97, 99

Итак, существует 9² = 81 двузначный номер без цифры 8. Но за каждым из них снова можно поставить любую из девяти допустимых цифр. В результате получим 9²9=9³ = 729 трехзначных номеров. Значит, в клубе было 729 велосипедистов. А если взять не трехзначные, а четырехзначные номера, то номеров, не содержащих восьмерок, будет 9⁴ = 6561.

Ответ: 6561 членов клуба.

Задача 35.

«В городе n светофоров. Каждый может находиться в одном из трех состояний (гореть красным, желтым или зеленым светом). Сколькими способами можно зажечь все светофоры?»

Решение.

Если есть только один светофор, то способов включения 3. Добавим теперь второй светофор. Из всякого способа включения одного светофора, изменяя состояние второго, мы можем получить три способа включения двух. Значит, число способов увеличится втрое. Итого: 33=3² способов. Добавим третий светофор. Из всякого способа включения двух светофоров снова можно получить три способа включения трех светофоров, изменяя состояние третьего. Снова число способов увеличится втрое. Для трех светофоров способов будет 33²=3³. При добавлении одного светофора число способов всегда увеличится втрое. Значит, n светофоров можно зажечь 3ⁿ способами.

Ответ: 3ⁿ.

Задача 36.

Секретный замок

Для запирания сейфов и автоматических камер хранения применяют секретные замки, которые открываются лишь тогда, когда набрано некоторое «тайное слово». Это слово набирают с помощью одного или нескольких дисков, на которых нанесены буквы (или цифры). Пусть на диск нанесены 12 букв, а секретное слово состоит из 5 букв. Сколько неудачных попыток может быть сделано человеком, не знающим «секретного слова»?

Решение.

Общее число комбинаций равно 12⁵ = 248832.

Значит, неудачных попыток может быть 248831. Впрочем, обычно делают сейфы так, что после первой же не удачной попытки открыть их раздается сигнал тревоги.

Ответ: 248831 попытка.

Задача 37.

«Сколькими способами можно зажечь n светофоров, из которых k могут находиться в одном из трех состояний, а остальные n—k в одном из двух?»

Решение.

Пусть первые k светофоров горят каким-то способом (таких способов 3^k), при этом остальные можно зажечь 2^n—k способами. Значит, из каждого способа включения k первых светофоров можно получить 2^n—k способов включения всех светофоров. Значит, всего способов 3^k2^n—k.

Ответ: 3^k2^n—k.

Задача 38.

Код Морзе

При передаче сообщений по телеграфу используется код Морзе. В этом коде буквы, цифры и знаки препинания обозначаются точками и тире. При этом для одних букв используется один знак, например Е●, а для некоторых приходится использовать пять знаков, например Э●● — ●●…

Откуда же взялось число 5? Нельзя ли обойтись меньшим числом знаков, скажем, передавать все сообщения с помощью комбинаций, содержащих не более четырех знаков? Оказывается, что нельзя, и ответ этот дает именно формула для числа размещений с повторениями. Только две буквы можно передать с помощью одного знака (Е● и Т—): . С помощью двух знаков можно передать 2² = 4 буквы, трех знаков — 2³ = 8 букв и четырех знаков — 2⁴ = 16. Поэтому общее число букв, которые можно передать четырьмя знаками, равно 2+4+8+16 = 30.

А в русском алфавите 32 буквы, да еще надо передавать цифры и знаки препинания. Ясно, что символов из четырех знаков не хватает. А если брать и символы из 5 знаков, то к полученным 30 прибавится еще 32 символа. Полученных 62 символов вполне достаточно для телеграфирования.

Применяют для телеграфирования и пятизначный код, в котором каждая буква изображается в точности пятью символами. Здесь уже вместо точек и тире используют перемены направления тока, или посылку токового и бестокового сигнала. При пользовании этим кодом имеем ровно 2⁵ = 32 комбинации. Их хватает для передачи букв. А для передачи цифр, знаков препинания и т. д. используют те же комбинации, что и для букв. Поэтому телеграфные аппараты пятизначного кода имеют специальное устройство для перевода аппарата с букв на цифры и обратно.

Задача 39.

«В некотором царстве каждые два человека отличаются набором зубов. Какова может быть наибольшая численность населения царства (максимальное количество зубов — 32).»

Решение.

Поставим в соответствие каждому жителю царства последовательность из 32-х нулей и единиц по следующему правилу: если у жителя есть первый зуб, то поставим на первое место последовательности 1, а если нет, то 0; если у жителя есть второй зуб, то поставим на второе место последовательности 1, а если нет, то 0; если у жителя и т. д. (мы предполагаем, что зубы раз и навсегда как-то занумерованы). Из условия ясно, что разным жителям будут поставлены в соответствие разные последовательности, поэтому максимальное число жителей в царстве равно просто числу таких последовательностей. А число таких последовательностей 2³². Кстати, 2³²≈4.000.000.000 (четыре миллиарда). Это больше нынешнего населения земного шара.

Ответ: 4.000.000.000 человек.

Задача 40

«Сколькими способами можно разместить 8 пассажиров в три вагона?»

Решение.

Перенумеруем пассажиров, в каком – либо порядке. Первого из 8 пассажиров можно поместить в любой из 3 вагонов. Для каждого из этих трёх способов размещения первого пассажира второго можно разместить тоже в любой из трёх вагонов. Следовательно, двух пассажиров в 3 вагона можно разместить 33 = 3² способами. Т.к. каждого следующего пассажира тоже можно разместить в любой из трёх вагонов, то 8 пассажиров в 3 вагона можно разместить 3⁸ числом способов.

Можно рассуждать и следующим способом. Сопоставив каждому пассажиру номер вагона, в котором он будет размещён, получим упорядоченный набор из 8 чисел. Например, набор (1,2,2,3,3,3,3,3) показывает, что первый пассажир будет в первом вагоне, два следующих пассажира во втором, и остальные в третьем вагоне. Следовательно, нужно посчитать, сколько можно составить таких наборов длины 8, элементы для которых берутся из множества Х ={1,2,3}. Иначе говоря, нужно сосчитать число элементов прямого произведения , n() = n(x)n(x)…n(x)=3⁸.

Через n(x) обозначено число элементов множества Х).

Примечание. Упорядоченные наборы длины k, составленные из элементов n – элементного множества X, называют размещениями с повторениями из n элементов по k, их число обозначают ; .

Ответ: 3⁸

Задача 41.

«Сколько различных слов можно получить, переставляя буквы слова а) математика, б) абракадабра, в) какао? (здесь словом назван любой набор букв)»

Решение.

а) В слове «математика» 10 букв, среди которых две буквы «м», две «т» и три буквы «а».

Рассмотрим какое-либо слово, составленное из букв слова «математика». Таких слов было бы Р₁₀, если бы все буквы были бы различными. Так как при перестановке одинаковых букв слово не меняется, а буквы «м» можно поменять местами Р₂ числом способов, буквы «т» — Р₂ числом способов и буквы «а» — Р₃ числом способов, то для каждого слова существует Р₂*Р₂*Р₃ перестановок букв, при которых это слово не изменится. Таким образом, сосчитав все перестановки из 10 элементов, мы каждое слово сосчитали Р₂*Р₂*Р₃ раз. Следовательно, различных слов получится .

б), так как в слове пять букв «а», две буквы «р», две буквы «б».

в) .

Примечание. В рассмотренной задаче пришлось искать число перестановок с повторениями. Если имеется n предметов, среди которых n₁ одинаковых предметов первого типа, n₂ одинаковых предметов второго типа, …, n_k одинаковых предметов k-го типа (n₁+n₂+…+n_k=n), то число перестановок с повторениями из n элементов может быть найдено по формуле

Ответ: 151200, 83160, 30

Задача 42.

«10 человек надо разбить на три группы соответственно по 2, 3, 5 человек в группе. Сколькими способами можно это сделать?»

Примечание. Можно заметить, что

Решение.

Разбиение можно осуществить следующим способом: выберем любых двух человек для первой группы (это можно сделать способами), для каждого из этих способов из 8 оставшихся выберем любых трёх для второй группы (это можно сделать способами), Оставшиеся 5 человек образуют третью группу. Итак, всего способов получим . При этом не имеет значения, с какой группы начинать разбиение.

Ответ: 2520

Задача 43.

«В кондитерской имеются пирожные шести различных видов. Сколькими способами можно составить набор из 4 пирожных?»

Решение.

Каждому набору из 4 пирожных поставим в соответствие последовательность из четырёх единиц и пяти нулей так, чтобы число единиц до первого нуля означает число выбранных пирожных первого вида, число единиц между первым и вторым нулями означает число выбранных пирожных второго вида и т.д., число единиц после пятого нуля означает число выбранных пирожных шестого вида. Так, например, последовательности I00I I00I соответствует выбор по I пирожному первого и шестого видов и двух пирожных третьего вида, а последовательности 00000I I I I – выбор четырех пирожных шестого вида. Теперь задачу можно сформулировать так: сколькими способами можно выбрать из 9 позиций (5 нулей и 4 единицы) 4 позиции для единиц.

Это можно сделать способами.

Можно было рассуждать иначе: подсчитать число перестановок из 9 элементов с повторениями .

Примечание. В задаче было найдено число сочетаний с повторениями из шести по четыре. Сочетаниями из n элементов по m с повторениями называются группы, содержащие m элементов, причем каждый элемент принадлежит одному из n типов. Проведя аналогичные рассуждения, можно показать, что число сочетаний из n элементов по m с повторениями равно или ,(где m единиц и n-1 нулей).

Ответ: 126 способов.

Задача 44.

«Девять перенумерованных шаров нужно разместить по трем ящикам так, чтобы в одном было пять шаров, а в другом – три, в третьем – один. Сколькими способами это можно сделать?»

Замечание. Теорема: .

Решение.

По постановке данная задача эквивалентна следующей: сколькими способами множество A из 9 элементов можно разбить на попарно непересекающихся три подмножества B₁, B₂, B₃, содержащих соответственно 5, 3, 1 элемент. По теореме это число способов равно .

Ответ: 504 способа

Задача 45.

Морской семафор

На флоте иногда применяют семафор флажками. Каждой букве при этом соответствует определенное положение флажков. Как правило, флажки находятся по разные стороны от тела сигнальщика. Однако при передаче некоторых букв (б, д, к, х, ю, я) оба флажка рас положены по одну и ту же сторону. Почему пришлось сделать такое исключение?

Ответ на этот вопрос дает та же формула размещений с повторениями. Дело в том, что различных положений каждого флажка пять — вниз отвесно, вниз наклонно, горизонтально, вверх наклонно и вверх отвесно. Так как у нас два флажка, то общее число комбинаций основных положений равно . При этом еще надо отбросить положение, когда оба флажка направлены вниз — оно служит для разделения слов. Всего получаем 24 комбинации, а этого недостаточно для передачи всех букв русского алфавита. Поэтому для некоторых букв и пришлось направить оба флажка в одну сторону.

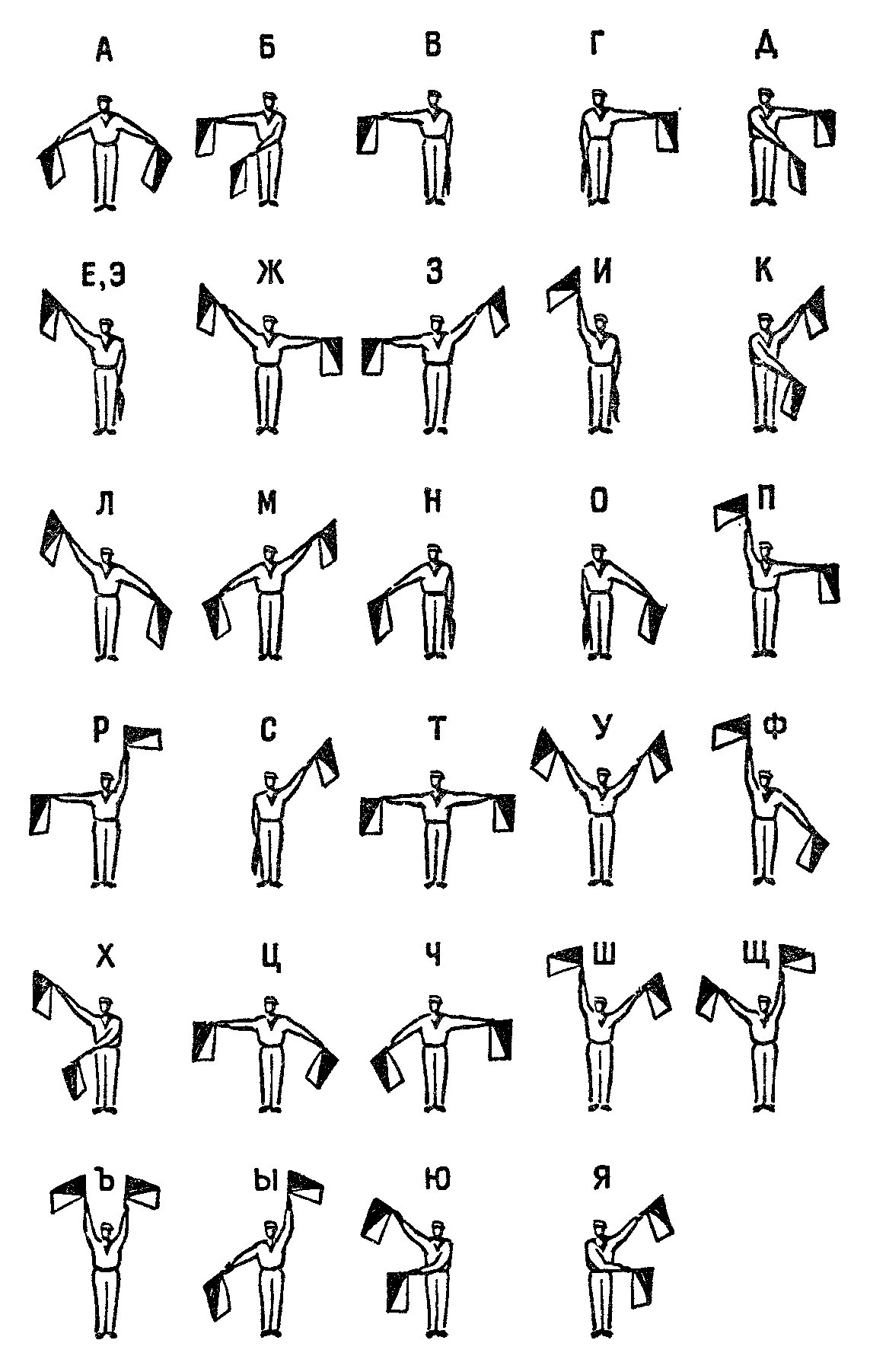
Задача 46.

«Сколько различных слов можно получить, переставляя буквы в слове «математика» (под словом здесь понимается любой набор состава (3,1,1,1,2,2) из букв (а, е, и, к, м, т))».

Решение.

.

Ответ: 151200 слов.

Задача 47.

«Сколько членов получится после раскрытия всех скобок в выражении: (a+1)(b+1)(c+1)(d+1)(e+1)(f+1)(g+1)?»

Решение.

Каждый из членов, которые получаются после раскрытия скобок в выражении (a+1)(b+1)(c+1)(d+1)(e+1)(f+1)(g+1), есть произведение семи сомножителей (так как скобок семь). Любой из этих сомножителей – либо буква, либо цифра 1. Итак, мы должны найти число произведений семи сомножителей, каждый из которых может быть «в двух состояниях». Значит, наша задача эквивалентна следующей: “Найти число способов освещения семью лампочками, каждая из которых может гореть или не гореть”. И получаем 2⁷

Ответ: 2⁷.

Задача 48.

Сколько существует телефонных номеров, содержащих комбинацию 12? (Номер состоит из шести цифр.)

Решение.

Рассмотрим пять множеств телефонных номеров (рис.13):

Рис.13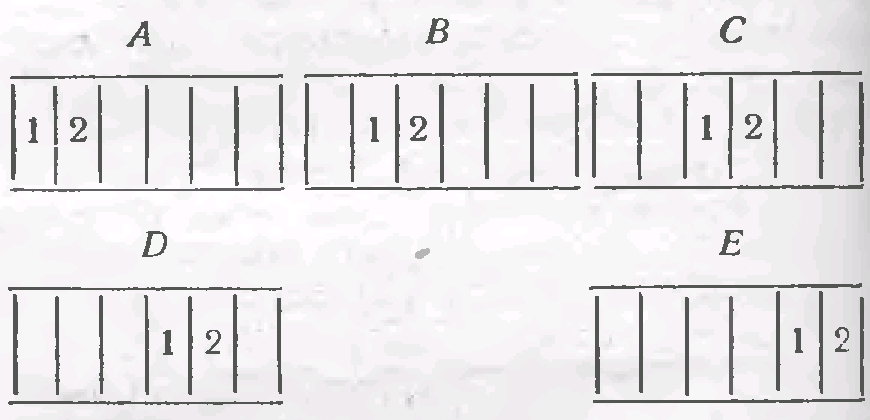

(Например, множество B состоит из номеров, у которых на втором-третьем месте стоит 12, а на остальных местах что угодно). В каждом из этих множеств по 10⁴ номеров. Множества A и B не имеют ни одного общего номера. Множества А и С имеют 10² общих номеров – это номера вида 1212_ _.

Легко подсчитать, что существует 610² номеров, которые входят одновременно в какие-нибудь два множества. И, наконец, только один номер (12 12 12) входит в три множества. Теперь легко показать, что искомое число равно 510⁴-610²+1=49401.

Ответ: 49401.

Задача 49.

Генетический код

Замечательным открытием биологии XX века была разгадка генетического кода. Удалось выяснить, каким образом наследственная информация передается потомству.

Оказалось, что эта информация записана в гигантских молекулах дезоксирибонуклеиновой кислоты (ДНК). Различные молекулы ДНК отличаются друг от друга тем, в каком порядке идут в них 4 азотистых основания: аденин, тимин, гуанин и цитозин. Эти основания определяют порядок построения белков организма из двух десятков аминокислот, причем каждая аминокислота зашифрована кодом из трех азотистых оснований.

Легко понять, откуда взялось число 3. Ведь с помощью комбинаций двух оснований можно зашифровать лишь 4²=16 аминокислот, а этого недостаточно. Если же брать по 3 основания, то получим 4³ = 64 комбинации. А этого с избытком хватит, чтобы зашифровать два десятка. Было бы весьма интересно узнать, как используется в природе избыточность информации — ведь число комбинаций равно 64, а число аминокислот втрое меньше.

В одной хромосоме содержится несколько десятков миллионов азотистых оснований. Число различных комбинаций, в которых они могут идти друг за другом, невообразимо велико. Ничтожной доли этих комбинаций достаточно было, чтобы обеспечить все разнообразие живой природы за время существования жизни на Земле. Разумеется, надо иметь в виду, что лишь ничтожная доля теоретически возможных комбинаций приводит к жизнеспособным организмам.

3. Задачи повышенной трудности

Задача 50.

Упростить:

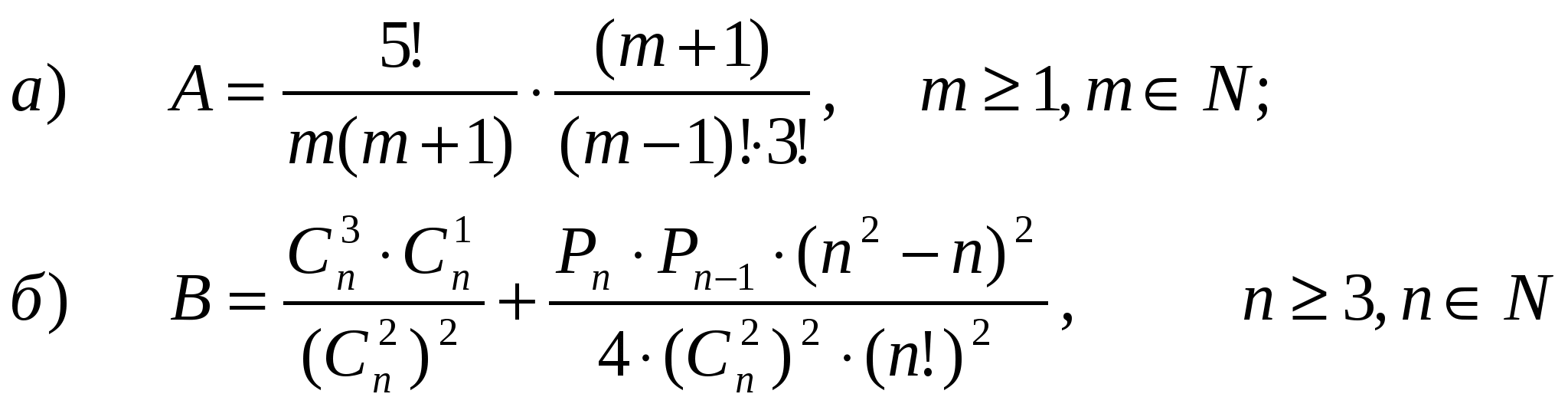
Решение.

а) Т.к. 5!=12345 = 3!45, (m+1)! = 12…(m-1)m(m+1)=(m-1)!m(m+1), то

б) Т.к. =n, , P_n=n!, P_n+1=(n+1)!, то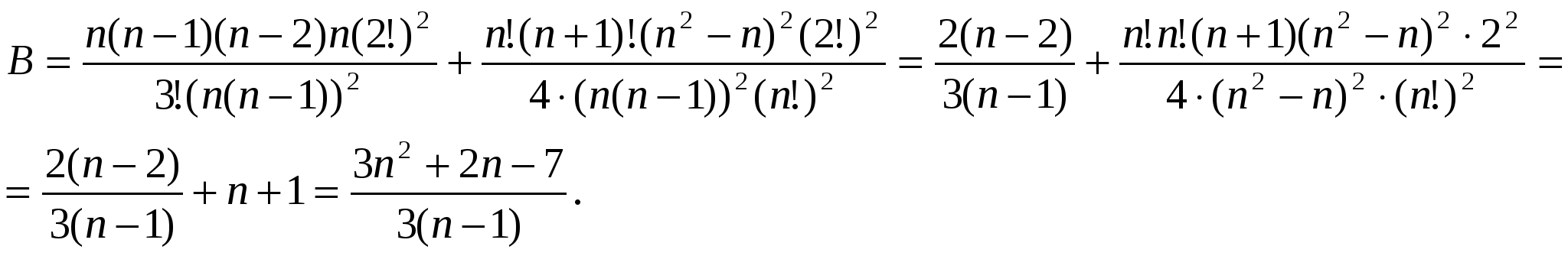

Ответ: а) 20, б)

Задача 51.

Найти все натуральные n, удовлетворяющие условию:

а) =14(n+1):

б) .

Решение.

а) Заметим, из условия n+1≥3, т.е. n≥2.

Используя свойство , можно записать . Имеем . Сократив на n+1N, получим

2n(n-1)+n=28 или 2n²—n-28=0. Решив уравнение получим, что натуральный корень n=4 удовлетворяет условию задачи.

б) Т.к. из условия n-1≥4 , n-2 ≥2, то n≥5.

Используя формулы и , получим

(n-2)(n-4)-4(n-1)-30<0; n²-9n-22<0; -2<n<11.

Т.к. n – натуральное и n≥5, то условию задачи удовлетворяют 5≤n≤10.

Задача 52.

«Пусть имеется n ламп. Число способов освещения, при которых горят k ламп, обозначим через . Доказать, ».

Решение.

Сколько имеется способов освещения, если есть n ламп? Подсчитаем это число двумя методами.

Первый метод. 0) Может не гореть ни одна лампа. Таких способов освещения (горят 0 ламп из n). Ясно, что =1 при любом n. Тем не менее, чтобы доказываемая формула выглядела «красиво», мы будем писать не 1, а .

1) Может гореть ровно 1 лампа из n. Таких способов освещения .

2) Через обозначено число способов освещения, при которых горят 2 лампы из n.

k) Когда горят k ламп из n, получаем способов освещения.

n) Наконец, могут гореть все n ламп. Таких способов освещения . (Снова ясно, что =1)

Итак, всего способов освещения:

Второй метод. Обозначим число способов освещения n лампами (каждая из которых может гореть или не гореть) через D_n. Докажем по индукции, что D_n=2ⁿ.

D₁ – число способов освещения при наличии одной лампы, очевидно, равно 2. Далее, D_n=2D_n-1 (каждый способ освещения (n-1)-й лампой порождает 2 способа освещения n лампами: n-я лампа может гореть и не гореть). Значит, из предположения D_n-1=2^n-1 вытекает, что D_n=2ⁿ. Итак, D_n=2ⁿ. Но выше мы показали, что .

Следовательно, .

Задача 53.

«В библиотеке числится некоторое число читателей (т.е. людей, которые прочитали хотя бы одну книгу этой библиотеки). Про любые k книг (l≤k<n) известно, сколько читателей прочитало их все. Как узнать, сколько читателей в библиотеке? (Всего в библиотеке n книг.)»

Решение.

Просуммируем число читателей, прочитавших данные k книг, по всем наборам из k книг. Полученную сумму обозначим через S_k. Докажем, что S=S₁—S₂+S₃—S₄+…+(-1)^n-1S_n и есть число читателей в библиотеке.

Возьмем читателя, прочитавшего ровно k книг, и посмотрим, какой вклад он вносит в каждое слагаемое суммы S. Без ограничения общности можно считать, что наш читатель прочитал первые k книг. В слагаемое S, наш читатель внесет вклад k(=), так как он входит в число читателей, прочитавших первую книгу, в число читателей, прочитавших вторую, третью, и т. д. k-ю книгу. В S₂ наш читатель внесет вклад , так как он входит в число читателей, прочитавших любую пару книг из первых k. Аналогично, в S_m наш читатель внесет вклад при m≤k и 0 при m>k. Значит, вклад нашего читателя в сумму S равен:

Но мы знаем, что =0 и . Значит, вклад нашего читателя в сумму S равен 1. Рассуждение применимо к любому читателю. Следовательно, S равно числу читателей библиотеки, что и требовалось доказать.

Задача 54.

В выражении (х-1)(x-2)(x-3)…(x-100) раскрыты скобки и приведены подобные. Найти коэффициент при x⁹⁹.

Решение.

Рассмотрим слагаемые, которые получатся после раскрытия скобок, но до приведения подобных. Каждое такое слагаемое есть произведение ста сомножителей, причем любой из этих сомножителей есть либо буква x, либо цифра. Первый сомножитель есть либо x, либо (-1), второй сомножитель есть либо x, либо (-2) и т. д. Нас интересуют только такие произведения, в которых 99 раз встречается x и 1 раз встречается число. Таких будет сто, так как число может встретиться на первом, на втором и т.д. на сотом месте.

Соответствующие произведения будут:

.

Значит, коэффициент при x⁹⁹ равен (в скобках стоит сумма членов арифметической прогрессии.

Ответ: коэффициент при x⁹⁹ равен .

Задача 55.

«Сколькими способами можно представить натуральное число n в виде суммы двух натуральных слагаемых?»

Примечание. Задачу эту можно понимать по-разному. Можно считать, что порядок слагаемых несуществен, а можно считать, что существен. Иными словами, можно считать, что 8=3+5 и 8=5+3 — это одно и то же разложение, а можно считать, что разные. Ответы тоже будут получаться разные. Предлагается решить обе задачи.

Решение.

а) Порядок существен. В этом случае каждое разложение определяется первым слагаемым, которое может быть любым натуральным числом, меньшим n (при этом и второе слагаемое будет натуральным числом). Значит, всего разложений будет n-1.

б) Порядок несуществен. Если n нечетно, то разложений вдвое меньше, чем в случае а), так как разложения n=1+(n-1) и n=(n-1)+1, n=2+(n-2) и n=(n-2)+2 и т.д. теперь считаются одинаковыми. Получаем .

Если же n четно, то для разложения не найдется пары, а для любого другого найдется. Отсюда получаем: .

Ответ: или .

Задача 56.

Доказать, что в треугольнике Паскаля сумма чисел, стоящих в (n+1)-й строке, равна 2ⁿ.

Доказательство.

Применим метод математической индукции. При n=1 (вторая строка) сумма чисел равна 2. Докажем, что сумма чисел в (n+1)-й строке вдвое больше, чем в n-й. Для этого напишем n-ю и (n+1)-ю строки треугольника Паскаля в следующем виде:

1 a b … f g 1

+1 1+a a+b … f+g g+1 1+0

Вычислим сумму чисел в (n+1)-й строке.

(0+1)+(1+a)+(a+b)+…+(f+g)+(g+1)+(1+0).

Для этого сложим сначала первые слагаемые каждой скобки, а затем вторые слагаемые. Получим:

(0+1+a+b+…+f+g+1)+(1+a+b+…+g+1+0)=2(1+a+b+…+f+g+1).

Слева стоит сумма чисел (n+1)-й строки, а справа — удвоенная сумма чисел n-й строки. Теперь ясно, что сумма чисел в (n+1)-й строке равна 2ⁿ.

Что и требовалось доказать.

Задача 57.

Обозначим через число способов, которыми можно зажечь k лампочек из n (каждая лампочка может быть в двух состояниях). Доказать, что число стоит на (k+1)-м месте (n+1)-й строки треугольника Паскаля.

Доказательство.

Докажем, что на (k+1)-м месте (n+1)-й строки треугольника Паскаля стоит . Доказывать будем индукцией по n. Для n=1 теорема верна. Действительно, во второй строке треугольника Паскаля на первом месте стоит 1= и на втором месте стоит 1=. Предположим, что теорема верна для n. Докажем, что тогда она верна и для n+1. Если k=0 или k=n+1, то теорема верна, так как , а в любой строке треугольника Паскаля на первом и последнем месте стоят единицы. Вспомним теперь, что есть число способов включения k ламп из n. Посмотрим, сколько есть способов включения k ламп из n+1. Если последняя лампа горит, то остальные могут гореть способами (из остальных ламп мы можем включить любые k-1). Если же последняя лампа не горит, то остальные можно включить способами. Тем самым доказано, что . По индуктивному предположению в (n+1)-й строке треугольника Паскаля стоят числа . А по определению треугольника Паскаля в следующей строке будут стоять числа: . По доказанному, эту строчку можно переписать так: . Это и означает, что теорема верна для n+1. Индукция окончена.

Что и требовалось доказать.

Задача 58.

В выражении (1+x)⁵⁶ раскрыты скобки и приведены подобные. Найти коэффициенты при x⁸ и x⁴⁸.

Решение.

Сравним два выражения: (1+x)⁵⁶ и (1+a₁)(1+a₂)…(1+a₅₆).

Если положить a₁=a₂=…=a₅₆=x, то второе выражение превратится в первое.

После раскрытия скобок в выражении (1+a₁)(1+a₂)…(1+a₅₆) будет членов, содержащих 8 букв. Любой из этих членов превратится в х⁸ при замене каждой буквы a₁, a₂,…, a₅₆ на х.

Значит, коэффициент при x⁸ в выражении (1+x)⁵⁶ (после раскрытия скобок и приведения подобных) равен .

Аналогично, коэффициент при x⁴⁸ равен .

Примечание. Числа и равны. Поэтому коэффициенты при x⁸ и при x⁴⁸ в выражении (1+x)⁵⁶ равны. Точно так же равны между собой коэффициенты при x⁵ и при x⁵⁰ в выражении (1+x)⁵⁶. Вообще, в выражении (1+x)ⁿ равны коэффициенты при x^k и при x^n—k; .

Ответ: .

Задача 59.

В выражении (х+y+z)ⁿ найти член, содержащий .

Решение.

Найдем сначала все члены с х^к. Напишем

Теперь в выражении найдем член с y^l: .

Отсюда ясно, что член, содержащий , будет . Выражение можно несколько преобразовать: .

Ответ: .

Задача 60.

Определить сумму коэффициентов многочлена, который получится, если в выражении (1+x-3x²)¹⁹⁶⁵ раскрыть скобки и привести подобные члены.

Решение.

Если в выражении (1+x-3x²)¹⁹⁶⁵ раскрыть скобки и привести подобные члены, получится многочлен . Заметим, что сумма его коэффициентов равна значению многочлена при х=1: .

Разумеется, на самом деле раскрывать скобки и приводить подобные не надо. Достаточно подставить х=1 в исходное выражение: (1+1-31²)¹⁹⁶⁵=(-1)1965=-1.

Итак, .

Ответ: .

4. Методические рекомендации

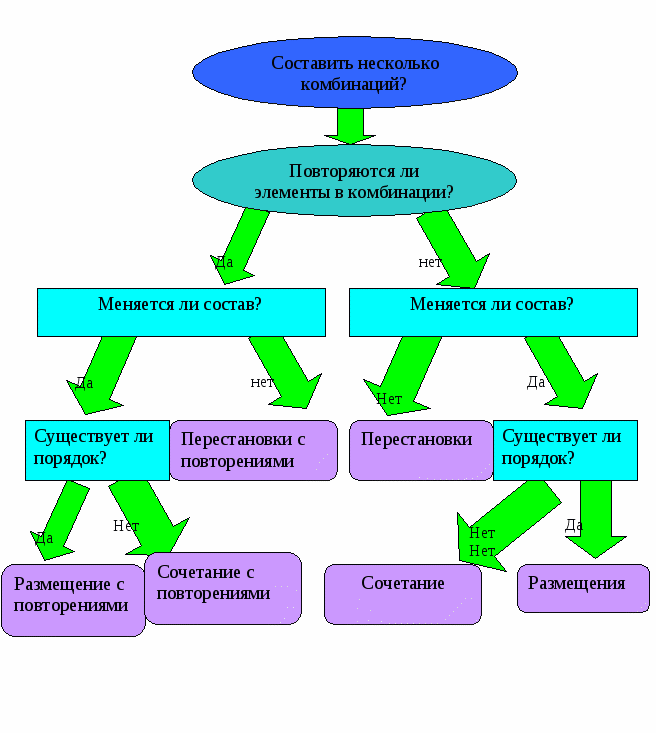
5. Библиографический список

1. Виленкин, Н.Я. Задачник-практикум по теории вероятностей с элементами комбинаторики и математической статистики/ Н.Я.Виленкин, В.Г.Потапов.-М: Просвещение, 1979.

2. Виленкин, Н.Я. Комбинаторика/ Н.Я.Виленкин, А.Н.Виленкин, П.А.Виленкин.-М: ФИМА, МЦНМО, 2006.

3. Гельфанд, С.И. Задачи по элементарной математике/ С.И.Гельфанд, М.Л.Гервер, А.А.Кириллов.- М: Наука, 1965.

4. Гусев, В.А. Внеклассная работа по математике в 6-8 классах/ В.А.Гусев, А.И.Орлов, А.Л.Розенталь.- М.: Просвещение, 1984.

5. Ежов, И.И. Элементы комбинаторики/ И.И.Ежов,А.В.Скороход, М.И.Ядренко.-М: Наука, 1977.

6. Солодовников, А.С. Теория вероятностей/ А.С.Солодовников.-М: Просвещение, 1983.

7. Тимофеенко, Г.В. Вводный курс математики/ Г.В.Тимофеенко, Е.Т.Астахова, Л.Г.Латынцева.-Красноярск: изд-во КГПУ, 1997.