Сценарий внеклассного мероприятия по математике «История математических открытий» 11 класс

Министерство образования Саратовской области

Государственное бюджетное образовательное учреждение

Саратовской области среднего профессионального образования

«Саратовский областной педагогический колледж»

Сценарий внеклассного мероприятия по математике

«История математических открытий»

для 11 класса

Составители:

преподаватель математики

Дубинина Лариса Владимировна,

преподаватель методики преподавания математики Близнюк Оксана Викторовна,

преподаватель математики и информатики Старостина Ольга Владимировна,

преподаватель математики и информатики Попова Елена Игоревна

Саратов 2012

Сценарий внеклассного мероприятия

Цель:

Познакомить студентов с историей некоторых математических открытий, с фактами биографий известных математиков, и роли их открытий в современной жизни.

Задачи:

• Воспитывать у студентов интерес к математическим дисциплинам.

• Способствовать всестороннему развитию личности студентов, развитию их познавательного интереса.

• Углубить и расширить имеющиеся у студентов знания о математике и математиках.

• Реализовать взаимосвязь с соответствующими учебными дисциплинами.

Порядок подготовки внеклассного мероприятия:

1. Выбор темы мероприятия.

2. Создание инициативной группы.

3. Анализ научно-методической литературы.

4. Определение состава выступающих студентов.

5. Подготовка практических заданий и вопросов к викторине.

6. Поиск и обработка видеоматериалов.

7. Создание презентации.

Место проведения мероприятия: конференц – зал.

Время проведения мероприятия: 60—70 мин.

Ход мероприятия:

Вступительное слово преподавателя.

(Используется презентация «Пифагор»)

Очень часто учителям математики задают один и тот же вопрос: «А зачем мне математика? Мне она в жизни не пригодится».

Сегодня мы постараемся ответить на этот вопрос, рассказав вам о жизни великих математиков и об истории математических открытий.

Слово «математика» пришло к нам из древнего языка: произошло от древнегреческих слов «математикэ» и «матема» — «познание, наука».

Математика – наука о количественных отношениях и пространственных формах действительного мира. И если есть упражнения для развития тела, то математика призвана развивать логическое мышление, внимание, тренировать мозг. Недаром ее называют «гимнастикой ума».

Математика – очень увлекательная, интересная и полезная наука. Она может стать захватывающим занятием не только для взрослых, но и для детей.

Послушаем несколько историй из жизни великих математиков.

О простом и сложном,

Об истинном и ложном

Правдивые истории,

Серьезные, шутливые

Про опыты начальные

И про умы пытливые,

Про важные события –

Великие открытия.

Наука об измерении расстояний, площадей, объемов, свойств различных геометрических фигур, греки назвали геометрией. Что означает в переводе с греческого слово «геометрия»? (Землемерие, гео — земля, метро – измерять).

Основу геометрии составляет система теорем, многие из которых изучаются уже в средней школе.

Постарайтесь узнать по подсказкам, о какой известной теореме идет речь. Подсказки:

• Эту теорему изучают в средней школе и называют «теоремой невесты».

• Теорема используется на каждом шагу при изучении геометрических вопросов.

• Частные случаи этой теоремы были известны некоторым народам до ее открытия.

• Ученый, сформулировавший данную теорему, родился на острове Самос. В молодости путешествовал по Египту, жил в Вавилоне, где имел возможность в течение 12 лет изучать астрономию и астрологию у халдейских жрецов.

• Этому ученому, кроме данной теоремы, приписывается еще ряд замечательных открытий, в том числе теорема о сумме внутренних углов треугольника.

У математиков арабского Востока эта теорема получила название «теорема невесты», за сходство чертежа с пчелкой, бабочкой, что по-гречески называлось нимфой. При переводе с греческого арабский переводчик, не обратив внимания на чертеж, перевел слово «нимфа» как «невеста», а не «бабочка».

Знаменитая теорема Пифагора звучит так: площадь квадрата, построенного на гипотенузе (т.е. большой стороне) прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах (меньших сторонах). По картине, иллюстрирующей эту теорему, сложена шутливая поговорка: «Пифагоровы штаны на все стороны равны». Изучение вавилонских клинописных таблиц и древнекитайских рукописей показало, что утверждение этой теоремы было известно задолго до Пифагора.

Вавилоняне еще за тысячу лет до рождения Пифагора знали, площадь большого квадрата на рисунке вдвое больше площади маленьких квадратов и использовали это знание для укладки паркета.

С помощью этого утверждения всегда можно вычислить длину наклонной линии, например, расстояние от вершины шеста до конца тени.

В данном случае шест выступает в роли одного катета, а тень — в роли другого катета. Достаточно измерить их длины и воспользоваться теоремой Пифагора.

В строительной практике египтяне использовали так называемый «египетский треугольник» — треугольник со сторонами 3,4,5. (египтяне знали, что указанный треугольник является прямоугольным и для него выполняется соотношение 3²+4²=5², т.е. как раз то, что утверждает теорема Пифагора.)

Заслуга греческого ученого состояла в том, что он открыл доказательство этой теоремы.

Просмотр мультфильма «Теорема Пифагора».(https://www.star.sospk.ru/page.php?22)

Мы сейчас познакомились с оригинальной трактовкой теоремы Пифагора. А кто из вас сможет сказать, как звучит ее современная формулировка?

Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. Но теорема – лишь малая толика достижений древнегреческого философа, религиозного и политического деятеля, основателя пифагоризма, математика.

Великий древнегреческий ученый Пифагор родился на острове Самос в VI веке до н. э.

Будущий великий математик и философ уже в детстве обнаружил большие способности к наукам. В молодости он побывал в Египте, где учился у жрецов. Говорят, что он был допущен в сокровенные святилища Египта, посетил халдейских мудрецов и персидских магов. Учеба Пифагора в Египте способствует тому, что он сделался одним из самых образованных людей своего времени. Здесь же он попадает в персидский плен. В плену Пифагор встречался с персидскими магами, приобщился к учению халдейских мудрецов. Они познакомили его со знаниями, накопленными восточными народами в течение многих веков: астрономией, астрологией, медициной, арифметикой.

Пробыв двенадцать лет в вавилонском плену, Пифагор возвращается на родину, чтобы приобщить к накопленным знаниям свой народ.

Пифагор имел красивую внешность, носил длинную бороду, а на голове золотую диадему. Пифагор это не имя, а прозвище, которое получил философ за то, что всегда говорил верно, убедительно, как греческий оракул. (Пифагор – «убеждающий речью».)

Он был первым человеком, который назвал себя философом. До него умные люди называли себя гордо и несколько высокомерно – мудрецами, что означало – человек, который знает. Пифагор же называл себя философом — тем, кто пытается найти, выяснить.

Около 530г. до н. э. Пифагор переехал в Кротон – греческую колонию в Южной Италии, где основал свою философскую школу, так называемый пифагорейский союз. В сферу интересов членов союза входили научные исследования, религиозно-филосовские искания, политическая деятельность. Они вели суровый образ жизни, превыше всего ценили самообладание, смелость, коллективную дисциплину.

В уставе школы авторство всех математических работ приписывалось самому учителю.

Дисциплина в школе была казарменная. Пифагор составил подробный список табу для членов своего ордена. Вот некоторые из них:

— воздерживайся от употребления в пищу бобов;
— не поднимай то, что упало;
— не прикасайся к белому петуху;
— не откусывай от целой булки;
— не ходи по большой дороге и др.

Излюбленной геометрической фигурой пифагорейцев была пентаграмма. Она служила им паролем, была символом здоровья, счастья. Чтобы приветствовать друг друга, они вычерчивали ее на песке. Фигура эта необычайно интересна. Если соединить ее вершины, то получится правильный пятиугольник – пентагон. Его диагонали, пересекаясь, делятся в отношении “золотого сечения”.

Деятельность союза была окружена тайной, поэтому никаких текстов от ранних пифагорейцев не осталось.

Пифагорейцы называли собственные исследования «математа», что означает «науки», и делили их на четыре части: арифметику, геометрию, астрономию и гармонию (учение о музыке). Главной считалась арифметика – наука о числах. Именно она лежала в основе геометрии, астрономии и гармонии.

В то время, когда Пифагор появился в Кротоне, там, как и в других городах Великой Греции, растет общественное неравенство. Пифагор выступает с развернутой проповедью нравственного содержания, в ней он высказал те нравственные правила, строгое исполнение которых приводит души заблудших к совершенству.

Вот некоторые из них: —

• Не делай никогда того, чего ты не знаешь, но научись всему, что следует знать, и тогда ты будешь вести спокойную жизнь;

• Переноси кротко свой жребий, каков он есть, и не ропщи на него;

• Приучайся жить без роскоши.

После такого выступления жители Кротона единодушно избирают Пифагора своеобразным духовным отцом города.

Со временем Пифагор прекращает выступления в храмах и на улицах, а учит уже в своем доме. Система обучения была сложной, многолетней. Желающие приобщиться к знанию должны были пройти испытательный срок от трех до пяти лет. Все это время ученики обязаны были молчать и только слушать учителя, не задавая никаких вопросов. В этот период проверялись их терпение, скромность.

Пифагор был не только учитель, но и исследователь. Исследователями становились и его ученики.

Важнейшей научной заслугой Пифагора считается систематическое введение доказательства в математику. Строго говоря, только с этого момента математика и начинает существовать как наука.

Пифагор развил теорию музыки и акустики, создав знаменитую «пифагорейскую гамму» и проведя эксперименты по изучению музыкальных тонов: найденные соотношения он выразил на языке математики.

В школе Пифагора впервые была высказана догадка о шарообразности Земли. Ранее пифагорейцы были убеждены, что Земля имеет сферическую форму и вместе с другими планетами, включая и Солнце, обращается вокруг центра космоса, так называемого «очага».

Достаточно глубоко исследовал Пифагор и математические отношения. Особое внимание он уделял числам и их свойствам. Посредством чисел он пытался осмыслить такие вечные категории бытия, как справедливость, смерть, постоянство, мужчина, женщина и прочее. Число для Пифагора было и материей, и формой Вселенной. Философские суждения Пифагора о числах стали основой науки нумерологии.

Не чужда была пифагорейцам и геометрическая интерпретация чисел. Они ввели понятия «треугольные» и «квадратные» числа. Древние греки любили изображать числа камешками, раскладывая их на морском берегу. Так, например, они выкладывали «треугольные» числа.

Как вы думаете, какие следующие «треугольные» числа?

Так выглядят «квадратные» числа. Мы сейчас называем их «квадратными» — например, мы говорим: четыре в квадрате – шестнадцать.

Какие следующие «квадратные» числа?

Пифагор обнаружил интересную связь между нечетными числами и «квадратными»: сумма последовательных нечетных чисел, начиная с единицы, обязательно будет «квадратным» числом! Например, 1+3=4; 1+3+5=9; 1+3+5+7=16 и так далее.

Пифагорейцы были увлечены построением правильных геометрических фигур с помощью циркуля и линейки. Увлеченные этим «строительством» они выстроили фигуры вплоть до правильного пятиугольника и озадачились тем, как с помощью все тех же циркуля и линейки построить следующую правильную фигуру – семиугольник? Надо сразу же сказать, что это им не удалось.

Но они не только сами озадачились, но и озадачили все разумное человечество, которое с циркулем и линейкой в руках, наморщив лбы, ринулось строить правильные семиугольники.

Не тут-то было! Эта задачка пифагорейцев оставалась неразрешимой более двух тысячелетий! Решил ее только в 1796г. 19-летний немецкий юноша Карл Фридрих Гаусс (1777-1855), прозванный позже королем математиков.

«Построил» семиугольник, юный гений случайно, занимаясь совсем другими вычислениями. Со времени возникновения задачи прошло более двух тысяч лет…

Вот сколько терпения и времени требуется иногда на решение!

Пифагору не была уготована спокойная старость. Рассказывают: «Килон, кротонский муж, по своему роду, славе и богатству происходил из первых граждан, но был в остальном человеком тяжелым, тиранического нрава, насильником и сеятелем смуты. Всячески желая присоединиться к пифагорейскому образу жизни, он пришел к Пифагору, когда тот был уже стариком, но был им отвергнут по указанным причинам. После этого он и его друзья начали яростную борьбу против Пифагора и его соратников».

Дома пифагорейцев были разгромлены и разграблены, многие из пифагорейцев погибли. Из-за этих событий Пифагор уехал в Метапонт, где, говорят, и окончил свою жизнь.

После смерти Пифагора, его ученики обосновались в разных городах Великой Греции и организовали там пифагорейские общества.

(использование презентации «Архимед»)

(слайд №1) Архимед — это удивительный человек, имя которого люди помнят уже более 2000 лет. Он был талантливым математиком, механиком и инженером. Каждому школьнику знакомо чиcло π, правило равновесия рычага, «золотое» правило механики, закон плавания тел и т.д. (слайд №2)

Имя Архимеда живёт в легендах.

Нам было интересно узнать о нём что-то новое.

Своими находками мы хотим поделиться с вами!

(слайд №3) Архимед родился в 287 году до н.э. в Сиракузах на острове Сицилия. Отец Архимеда — астроном и математик Фидий — состоял в близком родстве с Гиероном, тираном Сиракуз. Отец привил сыну с детства любовь к математике, механике и астрономии. (слайд №4)

В Александрии Египетской — научном и культурном центре того времени — Архимед познакомился со знаменитыми александрийскими учеными.

(слайд №5) Именно здесь Архимед познакомился с трудами Демокрита, Эвдокса и других выдающихся греческих геометров.

Покинув Александрию, Архимед вернулся в Сицилию. В Сиракузах он был окружён вниманием и не нуждался в средствах.

Из-за давности лет жизнь Архимеда тесно переплелась с легендами.

(слайд №6) Существует легенда о том, как царь Гиерон поручил Архимеду проверить, не подмешал ли ювелир серебра в его золотую корону. Целостность изделия нарушать было нельзя. Архимед долго не мог выполнить эту задачу.

Решение пришло случайно…(слайд №7)

Фрагмент мультфильма.( https://www.star.sospk.ru/page.php?22)

Закон Архимеда является основой гидравлики – науки, изучающей законы движения и равновесия жидкостей. (слайд №8)

Знание гидравлики позволило изобрести винтовой насос для выкачивания воды. Такой насос (кохля) до недавнего времени применялся на испанских и мексиканских серебряных рудниках. (слайд №9)

Фрагмент мультфильма.( https://www.star.sospk.ru/page.php?22)

Малому и старому знакомо Архимедово правило рычага. (слайд №10) Согласно преданию ученый произнес крылатую фразу: «Дайте мне точку опоры, и я переверну весь мир!» Конечно, Архимед имел в виду применение рычага, но, прямо скажем, он был несколько самоуверен: кроме точки опоры и рычага понадобился бы совершенно фантастический — невероятно длинный и при этом несгибаемый стержень. (слайд №11)

Достоверные факты и многочисленные легенды говорят о том, что Архимед изобрел немало интересных машин и приспособлений.

Царь Гирон приказал построить огромный корабль «Сиракосия». Но он был так тяжел, что множество воинов не могли сдвинуть его с места. Тогда Архимед сконструировал механизм, который позволил сделать это одному человеку. (слайд №12)

Фрагмент мультфильма.( https://www.star.sospk.ru/page.php?22)

Архимед был семидесятилетним стариком, когда римляме осадили его родной город Сиракузы. Чтобы помочь жителям в обороне, он изобретал военные машины. (слайд №13)

Фрагмент мультфильма.(https://www.star.sospk.ru/page.php?22)

Чтобы отразить нападение большого римского корабля, Архимед заставил греческих воинов до блеска отполировать металлические щиты, а затем выстроиться вдоль берега. (слайд №14) По его указанию воины сфокусировали солнечные лучи от щитов в одной точке на борту корабля. Деревянная обшивка судна нагрелась до высокой температуры и вспыхнула — на корабле начался пожар.

Но для самого ученого все эти военные изобретения были лишь незначительными практическими приложениями его научных открытий.

Главные математические достижения Архимеда касаются проблем, которые сейчас относят к области математического анализа.

Сохранившиеся сочинения Архимеда можно разделить на три группы: (слайд №15)

Первая группа — определение площадей криволинейных фигур или соответственно, объёмов тел.

Архимед нашёл общий метод, позволяющий найти любую площадь или объём. Он определил с помощью своего метода площади и объёмы почти всех тел, которые рассматривались в античной математике. (слайд №16)

Лучшим своим достижением он считал определение площади поверхности и объёма шара.

Идеи Архимеда легли в основу интегрального исчисления. (слайд №17)

Вторую группу составляют работы по геометрическому анализу статистических гидростатических задач:

«О равновесии плоских фигур».

Знаменитый закон гидростатики,

вошедший в науку как закон Архимеда, сформулирован в трактате «О плавающих телах».

На всякое тело, погруженное в жидкость, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости.

Закон Архимеда справедлив и для газов. (слайд №18)

К третьей группе можно отнести различные математические работы: Например, как среди цилиндров, вписанных в шар, найти цилиндр, имеющий наибольший объём? (слайд №19)

В работе «Об измерении круга» Архимед дал своё знаменитое приближение числа π: «архимедово число».

В древнем Египте считали, что 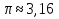(слайд №20)

В Древнем Риме считали, что 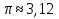(слайд №21)

(слайд №22) Архимед установил, что число больше 3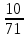 но меньше 3 Этот результат не уступает по точности той оценке, которую мы и сейчас не редко используем: .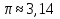

Задачи, решённые Архимедом, сложны и красивы сами по себе, но приёмы, используемые для их решения, оказались ещё более удивительными, чем ответы. Они послужили подсказкой учёным куда более поздней эпохи – первооткрывателям современного математического анализа. (слайд №23)

ПРО ЧИСЛО 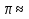3,1415926…

Гордый Рим трубил победу

Над твердыней Сиракуз,

Но трудами Архимеда

Много больше я горжусь.

Надо нынче нам заняться,

Оказать старинке честь,

Чтобы нам не ошибаться,

Чтоб окружность вечно счесть.

Надо только постараться

И запомнить все как есть:

Три-четырнадцать-пятнадцать,

Девяносто два и шесть!

(слайд №24) В 212 году до н.э. учёный погиб во время римской атаки. Но и после его смерти Сиракузы продолжали успешно обороняться, используя его изобретения.

О смерти Архимеда, также как о его жизни, тоже ходят легенды.

По первой, в разгар боя он сидел на пороге своего дома, углубленно размышляя над чертежами, сделанными им прямо на дорожном песке.

В это время пробегавший мимо римский воин наступил на чертёж, и возмущенный ученый бросился на римлянина с криком: «Не тронь моих чертежей!».

Эта фраза стоила Архимеду жизни. Солдат остановился и хладнокровно зарубил старика мечом.

(слайд №25) Вторая версия гласит, что полководец римлян Марцелл специально послал воина на поиски Архимеда.

Воин разыскал ученого и сказал:

— Иди со мной, тебя зовет Марцелл.

— Какой еще Марцелл?! Я должен решить задачу!

Разгневанный римлянин выхватил меч и убил Архимеда.

(слайд №26) Несомненно, Архимед – самый гениальный ученый Древней Греции. Он стоит в одном ряду с Ньютоном, Гауссом, Эйлером, Лобачевским и другими величайшими математиками всех времен. Он сделал замечательные открытия не только в математике, но и в механике, хорошо знал астрономию, оптику, гидравлику и был поистине легендарной личностью.

(использование презентации «Эйлер»)

(слайд №1) Научные результаты принадлежат всему человечеству. По крайней мере, это относится к естественным наукам, где результаты истинны или ошибочны вне зависимости от национальности и социального положения автора. И все- таки существует наука китайская, французская, российская…

Российская возникла благодаря петровскому «окну в Европу». Правда сам Петр не дожил до создания Академии, но через несколько месяцев после его смерти в 1725 году санкт- петербургская Академия Наук была открыта. В числе академиков было немало честолюбивых молодых западноевропейцев.

Одним из них был Леонард Эйлер, швейцарец по происхождению. (слайд №2)

Леонарда Эйлера часто называют идеальным математиком 18 века.

(слайд №3) Он родился и вырос в семье пастора в маленькой тихой Швейцарии, куда изо всей Европы приезжали мастера и ученые, не желавшие тратить дорогое рабочее время на гражданские смуты или религиозные распри.

Жил Эйлер в очень тихое время (всего за 6 лет до его рождения в Берлине была публично сожжена последняя ведьма, а через 6 лет после его смерти — в 1789 году — в Париже вспыхнула революция), в обстановке, всячески способствующей становлению великого гения.

За свою жизнь Эйлер добился столького, что сравниться он мог бы разве что с Ломоносовым (который, кстати, был его современником). Сфера интересов Эйлера огромна – он интересовался практически всеми науками, и несомненно преуспел в изучении каждой из них. Его деятельность оказала большое влияние на развитие математики, физики, астрономии… Научный авторитет этого человека по сей день не имеет границ.

Эйлер умер, будучи абсолютно слепым, но при этом (как Эйнштейн) ни на день не переставая работать. Его научное наследство необъятно. Шутя, Эйлер говорил, что оставит для академического журнала работ на 20 лет. В действительности, на этот раз он ошибся в расчетах – посмертно его труды печатали еще более 80 лет.

(слайд №4) Живший в двух странах – в Германии и в России – Эйлер покорил весь мир своим непревзойденным умом и уникальной трудоспособностью.

П. Лаплас говорил: “Читайте, читайте Эйлера, он наш общий учитель”.

(слайд №5) Эйлер, оставивший после себя более 800 научных трудов, интересовался почти всем, чем может интересоваться человек науки.

Последующие слайды расскажут об интересах и достижениях великого математика.

(слайд №6) Главным интересом всей жизни Эйлера была математика. Именно любовь к математике определила его судьбу во время обучения в Базельском университете на священника.

Эйлер постепенно шел к славе. Из его переписки с Иоганном Бернулли можно наблюдать, как рос его авторитет:

сначала Бернулли обращается к «учёнейшему и даровитейшему юному мужу Леонарду Эйлеру«,

через год — к «широко известному учёному«,

в 1737 г. — к «знаменитейшему и остроумнейшему математику«,

а в 1745 г. — к «несравненному Леонарду Эйлеру — главе математиков«.

Эйлер работал в Петербургской академии наук и в академии Фридриха II в Берлине, и неустанно творил, творил, творил…

Научное наследие Леонарда Эйлера колоссально.

С точки зрения математики, XVIII век — это век Эйлера;

Он ввёл в математику исключительно важную «функцию Эйлера» (слайд №7) и сформулировал с её помощью «теорему Эйлера». (слайд №8)

Благодаря Эйлеру в математику вошли удивительная по красоте «формула Эйлера». (слайд №9)

Эйлер получил основные уравнения вариационного исчисления и определил пути дальнейшего его развития, подведя главные итоги своих исследований в этой области в монографии Метод нахождения кривых линий, обладающих свойствами максимума или минимума (1744). Значительны заслуги Эйлера в развитии теории функций, дифференциальной геометрии, вычислительной математики, теории чисел. (слайд №10) Двухтомный курс Эйлера Полное руководство по алгебре (1770) выдержал около 30 изданий на шести европейских языках.

Он исследовал алгоритмы построения магических квадратов методом обхода шахматным конем. (слайд №11)

Первым предложил изображать множества в виде кругов. (слайд №12)

В геометрии Эйлер также оставил значительный след. (слайд №13) Появилось множество понятий, носящих его имя:

• Точки Эйлера

• Прямая Эйлера(слайд №14)

• Призма Эйлера

• Окружность Эйлера. (слайд №15)

Он искал в геометрии не столько новые изящные факты, сколько общие теоремы, не укладывающиеся в догматику Евклида. (слайд №16) Например, теорема о связи между числами вершин, ребер и граней выпуклого многогранника. Эту формулу знал еще Декарт; но он не оставил ее доказательства. Эйлер же установил и доказал, что числа вершин В, ребер Р и граней Г всякого многогранника, в котором нет «дыр», связаны формулой: сумма числа вершин и граней равна сумме ребер и числа 2.

(слайд №17) Леонард Эйлер является также основоположником теории графов, начало которой положило решение задачи о кенигсбергских мостах. В городе Кёнигсберге было два острова, соединенных семью мостами так, как показано на рисун-ке. Задача состояла в следующем: найти маршрут прохождения всех четырех частей суши (А, В С, Д), который бы начинался с любой из них, кончался на ней же и только один раз проходил по каждому мосту.

Эйлер доказал, что задача не имеет решений. Для этого он обозначил каждую часть суши точкой (вершиной), а каж-дый мост — линией (ребром). Получился граф, представленный на рисунке. Утверждение о невозможности на-хождения указанного маршрута эквивалентно утверждению о невозможности обойти граф указанным образом.

(слайд №18) Замечательны многочисленные работы Эйлера по небесной механике, среди которых наиболее известна его Новая теория движения Луны (1772), существенно продвинувшая важнейший для мореходства того времени раздел небесной механики.

Он вычислил возмущения Луны и опубликовал таблицы ее движения. Ведь в дальнем плавании Луна часто заменяла морякам часы при определении долготы.

(слайд №19) Вклад Леонарда Эйлера в мировую культуру и науку колоссален. И наша страна действительно гордится тем, что почти все потомки этого великого ученого приняли российское подданство, а некоторые его дальние родственники живут в России и по сей день.

Викторина «Занимательная математика» (использование презентации «Занимательная математика») https://www.star.sospk.ru/page.php?22

(использование презентации «Гаусс»)

(слайд №1) В историю Европы начало девятнадцатого века вошло как эпоха Наполеона. В историю европейской математики — как эпоха Гаусса.

(слайд №2) Величайший немецкий математик, астроном и физик родился в городе Брауншвейге (слайд №3) — столице одного из многочисленных гер-манских герцогств, княжеств и королевств того времени. (слайд №4) Его отец, садовник и фонтанный мастер, славился искусством быстро и легко считать. Эта способность перешла к сыну, говорившему позднее, что он «умел считать раньше, чем говорить».

(слайд №5) Первый успех пришел к Гауссу в 9 лет. Школьный учитель велел ученикам найти сумму чисел от одного до сорока, Он рассчитывал надолго занять учеников этой задачей. Но Гаусс мгновенно сообразил, как сгруппировать слагаемые, и выдал ответ:

1 + 40 + 2 + 39 + … + 20 + 21 = 41*20 = 820.

(слайд №6) О Гауссе узнают при дворе. В 1791 году его представляют Карлу Вильгельму Фердинанду — герцогу Брауншвейгскому. Мальчик бывает во дворце и развлекает придворных искусством счета. Благодаря покровительству герцога Гаусс смог в октябре 1795 года поступить в Геттингенский университет. (слайд №7) Первое время он слушает лекции по филологии и почти не посещает лекций по математике. Но это не означает, что он не занимается математикой. В 1795 году Гаусса охватывает страстный интерес к целым числам. Незнакомый с какой бы то ни было литературой, он должен был все создавать себе сам. И здесь он вновь проявляет себя как незаурядный вычислитель, пролагающий пути в неизвестное. (слайд №8) Осенью того же года Гаусс переезжает в Геттинген и прямо-таки проглатывает впервые попавшуюся ему литературу: Эйлера и Лагранжа.

Некоторое время Гаусс уже занимался группировкой корней из единицы на основании своей теории «первообразных» корней. (слайд №9) И вот однажды утром, проснувшись, он внезапно ясно и отчетливо осознал, что из его теории вытекает построение семнадцатиугольника… Это событие явилось поворотным пунктом жизни Гаусса. Он принимает решение посвятить себя не филологии, а исключительно математике. Сам Гаусс сохранил трогательную любовь к своему первому открытию на всю жизнь. Подобно Архимеду Гаусс выразил желание, чтобы в памятнике на его могиле был увековечен семнадцатиугольник.

30 марта 1796 года, в день, когда был построен правильный семнадцатиугольник, начинается — летопись его замечательных открытий. Следующая запись в дневнике появилась уже 8 апреля. (слайд №10) В ней сообщалось о доказательстве теоремы квадратичного закона взаимности, которую он назвал «золотой».

Весь нелегкий путь к «золотой теореме» он прошел самостоятельно. Два великих открытия Гаусс сделал на протяжении всего десяти дней, за месяц до того, как ему исполнилось 19 лет! Одна из самых удивительных сторон «феномена Гаусса» заключается в том, что он в своих первых работах практически не опирался на достижения предшественников, открыв как бы заново за короткий срок то, что было сделано в теории чисел за полтора века трудами крупнейших математиков.

(слайд №11) В 1798 году Гаусс подготовил диссертацию, посвященную доказательству основной теоремы алгебры, утверждения о том, что всякое алгебраическое уравнение имеет корень, который может быть числом действительным или мнимым, одним словом – комплексным.

 «Математический век» Гаусса — менее десяти лет. (слайд №12) При этом большую часть времени заняли работы, оставшиеся неизвестными современникам (эллиптические функции). Гаусс считал, что может не торопиться с публикацией своих результатов, тридцать лет так и было. (слайд №13). Но в 1827 году сразу два молодых математика — Абель и Якоби — опубликовали многое из того, что было им получено. О работах Гаусса по неевклидовой геометрии узнали лишь при публикации посмертного архива.

(слайд №14) Новым увлечением Гаусса стала астрономия. Главная причина занятия его новой наукой была прозаической. Получить где-нибудь кафедру по математике было не просто, да Гаусс и не очень стремился к активной преподавательской деятельности. Расширяющаяся сеть обсерваторий делала карьеру астронома более доступной.

(слайд №15) Благодаря его расчетам, удается открыть первые астероиды — малые планеты между Марсом и Юлитером, Санкт-Петербургская академия наук приглашает Гаусса на должность директора обсерватории. Однако, вскоре после этого обсерватория была организована в Геттингене. И Гаусс остался там, не подозревая, что через несколько лет Германия будет по частям завоевана Наполеоном, что его покровитель, герцог Брауншвейгский, погибнет в бою, а самому Гауссу предстоят несколько лет тяжелейшей жизни в условиях оккупации.

(слайд №16) В 1809 году выходит знаменитая «Теория движения небесных тел, обращающихся вокруг Солнца по коническим сечениям». (слайд №17). Гаусс излагает свои методы вычисления орбит. Чтобы убедиться в силе своего метода, он повторяет вычисление орбиты кометы 1769 года, которую в свое время за три дня напряженного счета вычислил Эйлер. Гауссу на это потребовался час. В книге был изложен метод наименьших квадратов, остающийся по сей день одним из самых распространенных методов обработки результатов наблюдений.

(слайд №18) На 1810 год пришлось большое число почестей: Гаусс получил премию Парижской академии наук и золотую медаль Лондонского королевского общества, был избран в несколько академий.

Регулярные занятия астрономией продолжались почти до самой смерти. Знаменитую комету 1812 года (которая «предвещала» пожар Москвы) всюду наблюдали, пользуясь вычислениями Гаусса.

(слайд №19) К 1820 году центр практических интересов Гаусса переместился в геодезию. Это было связано с поручением произвести геодезическую съемку Ганноверского королевство и составить детальную его карту.

(слайд №20) Выполнение геодезической съемки требовало усовершенствованной оптической сигнализации, для которой ученый изобрел специальный прибор – гелиотроп.

В конце жизни Гаусса болыпе вссго интересует физика. Ему принадлежат фундаментальные открытия в теории электричества и магнетизма.

(слайд №21) Умер Гаусс 23 февраля 1855 года.

А теперь предлагаем вам выполнить задание (слайд №22).

По какому принципу нужно произвести вычисление?

Ответ — (слайд №23)

(Далее используется презентация «Лобачевский»)

Русские, в силу целого ряда исторических причин, поздно вступили на путь математического творчества, но первый же шаг на этом пути оказался столь крупным, что без всякого преувеличения можно сказать – он в значительной степени определил дальнейшее развитие не только математики, но и других наук. Этот шаг был сделал Николаем Ивановичем Лобачевским.

Будущий великий математик родился в ноябре 1792 г. в Нижегородской губернии в бедной семье мелкого чиновника. Отцом его считают макарьевского землемера отставного капитана Сергея Шебаршина. Брак родителей не был оформлен, и Лобачевский носил фамилию матери Прасковьи Александровны Лобачевской.

Детство Лобачевского было тяжелым и бедным. В Казанской гимназии он был казеннокоштным студентом, что накладывало определенные обязанности и ограничения. Самым простым было учиться лучше других; но казеннокоштным студентам, например, не разрешалось выходить дальше, чем за пределы парадного двора. Но уже с самого начала жизни Лобачевский интересовался геометрией. Это неудивительно, ведь его отец был землемером. Лобачевский проявил также большую склонность к языкам – например, французский он выучил за три месяца . Он писал стихи – его поэмы о Волге считаются одними из лучших.

В 1811 г. Лобачевский получил степень магистра, в 1816 г. стал экстраординарным, а в 1822г. – ординарным профессором.

Лобачевский пользовался уважением и любовью студентов и коллег. Когда упразднили должность директора университета, то его кандидатуру на пост главного ректора утвердили без возражений. Не высказался даже его главный соперник – Симонов.

Во время эпидемии холеры, превратил университет в мини-госпиталь – из-за чего умерло гораздо меньше студентов, чем в других ВУЗах.

В 1842 году, во время большого пожара в Казани он героически спас древние книги.

Когда негде было разместить второй класс Казанской гимназии, он предложил свой дом , обещав потом построить для гимназии дворец. В 1845 году он получил должность управляющего Казанским учебным округом, а после стал член – корреспондентом Гуттенгенского университета.

В 1826г. Лобачевский совершил открытие (труд «О началах геометрии»), перевернувшее все существовавшие тогда представления о природе пространства, в основе которых более 2 тысяч лет лежало учение древнегреческого математика Евклида.

Люди занимались геометрией с глубокой древности, но в виде стройной логической системы она впервые была изложена только III в. до P.X. замечательным греческим математиком Евклидом. В основе всей геометрии Евклида лежало несколько простых первоначальных утверждений, которые принимались за истинные без доказательств . Эти утверждения , так называемые аксиомы , описывали свойства основных понятий и казались поначалу на столько очевидными , что не вызывали сомнений. Из этих аксиом путем доказательств выводились более сложные: таким образом, строилось все знание геометрии.

Когда в последующее века математика обрела вид строгой науки, были сделаны многочисленные попытки доказать Евклидовы аксиомы.

Особый интерес математиков всегда вызывала пятая аксиома о параллельных прямых, которая гласит : в данной плоскости к данной прямой можно через данную , не лежащую на этой прямой , точку провести только одну параллельную прямую. В отличие от остальных аксиом элементарной геометрии, аксиома параллельных не обладает свойством непосредственной очевидности, хотя бы потому что является высказыванием о всей бесконечной прямой в целом, тогда как в нашем опыте мы сталкиваемся только с большими или меньшими отрезками прямых. Поэтому на всем протяжении истории геометрии – от древности до первой части XIX века – имели место попытки доказать аксиому параллельных, то есть вывести ее из остальных аксиом геометрии.

С таких попыток начал и Лобачевский. Чтобы доказать пятую аксиому, он принял противоположное этой аксиоме допущение, что к данной прямой через данную точку можно провести бесконечное множество параллельных прямых.

Лобачевский пытался привести это допущение к противоречию с другими аксиомами Евклида, однако по мере того как он развертывал из сделанного им допущения все более и более длинную цепь следствий, ему становилось ясным, что никакого противоречия не только не получается, но и не может получиться. Вместо противоречия Лобачевский получил хоть и своеобразную, но логически совершенно стройную и безупречную систему положений, обладающую тем же логическим совершенством , что и обычная Евклидова геометрия. Эта система положений и составила так называемую неевклидову геометрию, или геометрию Лобачевского. Некоторые положения этой геометрии вы видите на слайдах.

И стояла геометрия Евклида,

Как египетское чудо – пирамида.

Строже выдумать строенья невозможно,

Лишь одна была в ней глыба ненадежна.

Аксиома называлась «Параллели».

Разгадать ее загадку не сумели.

И подумал Лобачевский:

«Но ведь связана

С природой аксиома!

Мы природу понимаем

По-земному.

Во Вселенной растоянья неземные,

Могут действовать законы там иные!

Да, конечно, да!

Доказывать бесцельно!

Параллельные пойдут непараллельно!

Там, где звездный мир

Раскинулся без края, —

Аксиома параллелей там другая!

Параллельна геометрия Евклида.

Есть еще одна –

Совсем другого вида».

Смотрел он долго в зимнее окно:

Горели звезды

В небе над Казанью.

Вселенная была с ним заодно –

Открылся чистый купол мирозданья.

И звезды в вышине огнем горели,

Твердя: непараллельны параллели.

А математика отправили в отставку.

Забытый всеми, быстро угасал,

Ослеп, но труд упрямо диктовал,

Внося то добавленье, то поправку.

О чем он думал

В свой последний час?

Быть может, о пространствах

Беспредельных,

Где нет привычных людям

Параллельных,

Иль думал он о будущем,

О нас?

И физика в дальнейшем подтвердила:

Теория его не миф, не сон.

Луч света не прямой. Вблизи светила

Он силой тяготенья искривлен.

Большой научный интерес представляют его труды по математического анализу, алгебре, теории вероятностей, механике, физике, астрономии.

Однако геометрия Лобачевского не была признана при жизни ученого. Сред и математиков с мировым именем только Гаусс оценил значение работ Лобачевского. Только в 60-х годах XIX века неевклидовой геометрией заинтересовалось новое поколение математиков. В 1868 году непротиворечивость геометрии Лобачевского была доказана итальянцем Э.Бельтрами.

Умер Н.И. Лобачевский в возрасте 64 лет в Казани.

-забытый царем, лишившись орденов и квартиры – ордена украли, а квартиру конфисковали. В его формулярном листе за сорок лет работы в графе отпусков бисерным подчерком Лобачевского было написано : «Не был».

Ему поставлен памятник – и поэт В.Фирсов написал о нем:

Высокий лоб, нахмуренные брови,

В холодной бронзе – отраженный луч…

Но даже неподвижный и суровый,

Он, как живой ,- спокоен и могуч.

Когда – то здесь, на площади широкой,

Задумчивый ,неторопливый, строгий,

Он шел на лекции – великий и живой.

Пусть новых линий не начертят руки,

Он здесь стоит, взнесенный высоко,

Как утверждение бессмертья своего,

Как вечный символ торжества науки.

Викторина «Великие математики» (использование презентации «Великие математики» https://www.star.sospk.ru/page.php?22)

НАШ ЮНЫЙ ДРУГ!

Сегодня вспомнишь формулу Герона,

Какую ты не раз писал.

Ты вспомнишь также и Ньютона,

Бином которого познал.

Пусть в памяти твоей воскреснет Архимед,

Сраженный за великие творенья.

Пусть вспомнится известный всем Виет,

Открывший формулу для уравненья.

Тебе знаком талантливый Декарт –

Систем координат создатель.

Ты знаешь Лобачевского, он, брат,

Коперник геометрии, творец, ваятель.

Запомни то, что Гаусс всем сказал:

«Наука математика – царица всех наук»,

Не зря поэтому он завещал –

Творить в огне трудов и мук.

Пусть ты не станешь Пифагором,

Каким хотел бы, может быть!

Но будешь ты учителем, а может, и ученым,

И будешь честно Родине служить!

Список используемой литературы

Бородин А.И., Бугай А.С. Биографический словарь деятелей в области математики – К.: Радянська школа, 1979.

Гончарова Л.В. Предметные недели в школе. Математика — Волгоград: Учитель, 2004.

Дьячкова Г.Т. Математика. Внеклассные занятия в начальной школе — Волгоград: Учитель, 2007.

Иченская М.А. Отдыхаем с математикой – Волгоград: Учитель, 2006.

Математика от А до Я. Энциклопедический словарь для юношества. Сост. Савин А.П. – М., Педагогика-пресс, 2001.

Мусский С.А. Сто великих людей – М., Вече, 2007.

Рыжов К. Сто великих россиян – М., Вече, 2006.

Ушакова О.Д. Великие ученые. Справочник школьника – Санкт-Петербург, Литера, 2005.

Я познаю мир. Детская энциклопедия. Математика. – Москва АСТ, 1997.

Для воспроизведения видео в презентация «Пифагор» и «Архимед» скачайте файлы видео по указанной ссылке и поместите их в папку с презентациями.